Data Structs
The diagram below represents the transformation from a rollup payload to the different structs that are allowed to be dispersed.
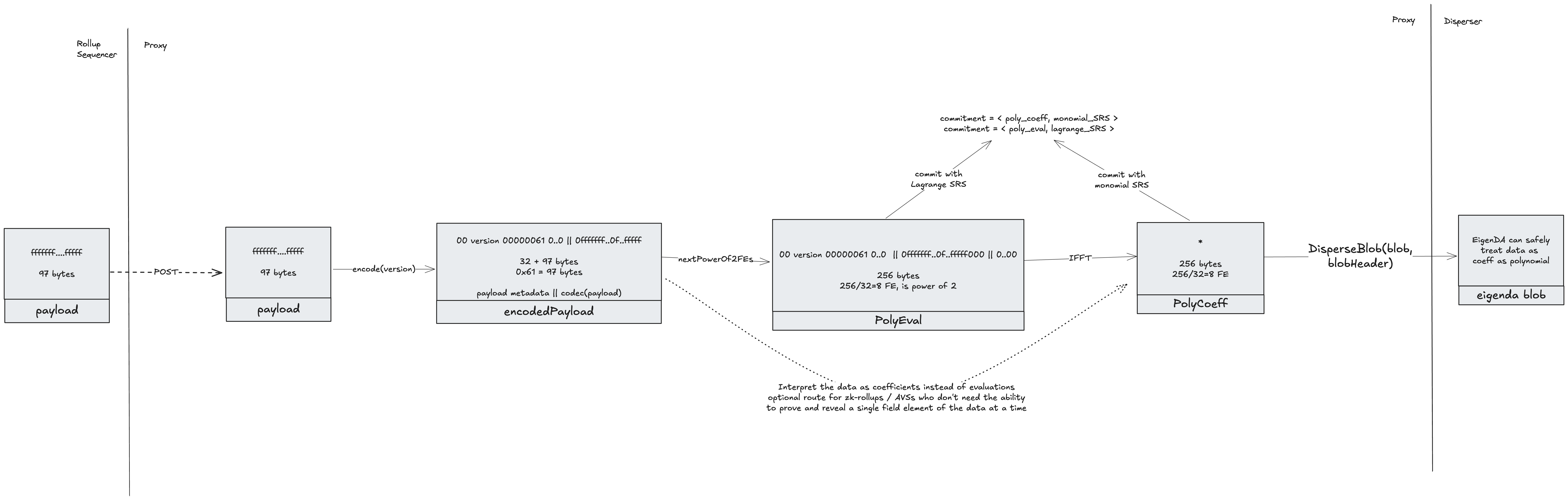
Payload
A client payload is whatever piece of data the EigenDA client wants to make available. For optimistic rollups this would be compressed batches of txs (frames). For (most) zk-rollups this would be compressed state transitions. For AVSs it could be Proofs, or Pictures, or any arbitrary data.
A payload must fit inside an EigenDA blob to be dispersed. See the allowed blob sizes in the Blob section.
EncodedPayload
An encodedPayload is the bn254 encoding of the payload, prefixed with an encoded payload header. It is an intermediary processing artifact, named here for clarity. The encoding obeys the same constraints as EigenDA blobs:
Every 32 bytes of data is interpreted as an integer in big endian format. Each such integer must stay in the valid range to be interpreted as a field element on the bn254 curve. The valid range is 0 <= x < 21888242871839275222246405745257275088548364400416034343698204186575808495617.
Encoded Payload Header
The header carries metadata needed to decode back to the original payload. Because it is included in the encoded payload, it too must be representable as valid field elements. The header currently takes 32 bytes: the first byte is 0x00 (to ensure it forms a valid field element), followed by an encoding version_byte and 4 bytes representing the size of the original payload. The golang payload clients provided in the eigenda repo currently only support encoding version 0x0. The remaining 26 bytes must be zero.
Encoding Payload Version 0x0
Version 0x0 specifies the following transformation from the original payload to a sequence of field element:
- For every 31 bytes of the payload, insert a zero byte to produce a 32-byte value that is a valid field element.
- Further pad the output above so the final length is a multiple of 32 bytes, and comprises a power-of-two number of 32-byte field elements (32, 64, 128, 256, …) to match EigenDA blob sizing. All of the padding must be 0.
[0x00, version_byte, big-endian uint32 len(payload), 0x00, 0x00,...] +
[0x00, payload[0:31], 0x00, payload[32:63],...,
0x00, payload[n:len(payload)], 0x00, ..., 0x00]
For example, the payload hello would be encoded as
[0x00, 0x00, 0x00, 0x00, 0x00, 0x05, 0x00, 0x00,...] +
[0x00, 'h', 'e', 'l', 'l', 'o', 0x00 * 26]
PayloadPolynomial
EigenDA uses KZG commitments, which represent a commitment to a function. Abstractly speaking, we thus need to represent the encodedPayload as a polynomial. We have two choices: either treat the data as the coefficients of a polynomial, or as evaluations of a polynomial. In order to convert between these two representations, we make use of FFTs which require the data to be a power of 2. Thus, PolyEval and PolyCoeff are defined as being an encodedPayload and interpreted as desired.
Once an interpretation of the data has been chosen, one can convert between them as follows:
PolyCoeff --FFT--> PolyEval
PolyCoeff <--IFFT-- PolyEval
Whereas Ethereum treats 4844 blobs as evaluations of a polynomial, EigenDA instead interprets EigenDA blobs as coefficients of a polynomial. Thus, only PolyCoeffs can be submitted as a blob to the Disperser. Each rollup integration must thus decide whether to interpret their encodedPayloads as PolyCoeff, which can directly be dispersed, or as PolyEval, which will require IFFT’ing into a PolyCoeff before being dispersed.
Typically, optimistic rollups will interpret the data as being evaluations. This allows creating point opening proofs to reveal a single field element (32 byte chunk) at a time, which is needed for interactive fraud proofs (e.g. see how optimism fraud proves 4844 blobs). ZK rollups, on the flip side, don't require point opening proofs and thus can safely save on the extra IFFT compute costs and instead interpret their data as coefficients directly.
Blob
A blob is a bn254 field elements array that has a power of 2. It is interpreted by the EigenDA network as containing the coefficients of a polynomial (unlike Ethereum which treats blobs as being evaluations of a polynomial).
An encodedPayload can thus be transformed into a blob directly or optionally by taking IFFT on itself, with size currently limited to 16MiB. There is no minimum size, but any blob smaller than 128KiB will be charged for 128KiB.
BlobHeader
The blobHeader is submitted alongside the blob as part of the DisperseBlob request, and the hash of its ABI encoding (blobKey, also known as blobHeaderHash) serves as a unique identifier for a blob dispersal. This identifier is used to retrieve the blob.
The BlobHeader contains four main sections that must be constructed. It is passed into the DisperseBlobRequest and is signed over for payment authorization.
Refer to the eigenda protobufs for full details of this struct.
Version
The blobHeader version refers to one of the versionedBlobParams structs defined in the EigenDAThresholdRegistry contract.
QuorumNumbers
QuorumNumbers represents a list of quorums required to sign and make the blob available. Quorum 0 represents the ETH quorum, quorum 1 represents the EIGEN quorum — both are always required. Custom quorums can also be added to this list.
BlobCommitment
The BlobCommitment is a binding commitment to an EigenDA Blob. Due to the length field, a BlobCommitment uniquely represents a single Blob. The length field is added to the kzgCommitment to respect the binding property. It is used by the disperser to prove to EigenDA validators that the chunks they received belong to the original blob (or its Reed-Solomon extension).
message BlobCommitment {
// A G1 commitment to the blob data.
bytes commitment = 1;
// A G2 commitment to the blob data.
bytes length_commitment = 2;
// Used with length_commitment to assert the correctness of the `length` field below.
bytes length_proof = 3;
// Length in bn254 field elements (32 bytes) of the blob. Must be a power of 2.
uint32 length = 4;
}
Unlike Ethereum blobs which are all 128KiB, EigenDA blobs can be any power of 2 length between 32KiB and 16MiB (currently), and so the commitment alone is not sufficient to prevent certain attacks:
-
Why is a commitment to the length of the blob necessary?
There are different variants of the attack. The basic invariant the system needs to satisfy is that with the chunks from sufficient set of validators, you can get back the full blob. So the total size of the chunks held by these validators needs to exceed the blob size. If I don't know the blob size (or at least an upper bound), there's no way for the system to validate this invariant. Here’s a simple example. Assume a network of 8 DA nodes, and coding ratio 1/2. For a
blobcontaining 128 field elements (FEs), each node gets 1282/8=32 FEs, meaning that any 4 nodes can join forces and reconstruct the data. Now assume a world without length proof; a malicious disperser receives the same blob, uses the same commitment, but claims that the blob only had length 4 FEs. He sends each node 42/8=1 FE. The chunks submitted to the nodes match the commitment, so the nodes accept and sign over the blob’s batch. But now there are only 8 FEs in the system, which is not enough to reconstruct the original blob (need at least 128 for that).
Note that the length here is the length of the blob (power of 2), which is different from the payload_length encoded as part of the
PayloadHeaderin theblobitself (see the encoding section).
PaymentHeader
The paymentHeader specifies how the blob dispersal to the network will be paid for. There are 2 modes of payment, the permissionless pay-per-blob model and the permissioned reserved-bandwidth approach. See the Payments release doc for full details; we will only describe how to set these 3 fields here.
message PaymentHeader {
// The account ID of the disperser client. This should be a hex-encoded string of the ECDSA public key
// corresponding to the key used by the client to sign the BlobHeader.
string account_id = 1;
// UNIX timestamp in nanoseconds at the time of the dispersal request.
// Used to determine the reservation period, for the reserved-bandwidth payment model.
int64 timestamp = 2;
// Total amount of tokens paid by the requesting account, including the current request.
// Used for the pay-per-blob payment model.
bytes cumulative_payment = 3;
}
Users who want to pay-per-blob need to set the cumulative_payment. timestamp is used by users who have paid for reserved-bandwidth. If both are set, reserved-bandwidth will be used first, and cumulative_payment only used if the entire bandwidth for the current reservation period has been used up.
NOTE: There will be a lot of subtleties added to this logic with the new separate-payment-per-quorum model that is actively being worked on.
An RPC call to the Disperser's GetPaymentState method can be made to query the current state of an account_id. A client can query for this information on startup, cache it, and then update it manually when making dispersals. In this way, it can keep track of its reserved bandwidth usage and current cumulative_payment and set them correctly for subsequent dispersals.
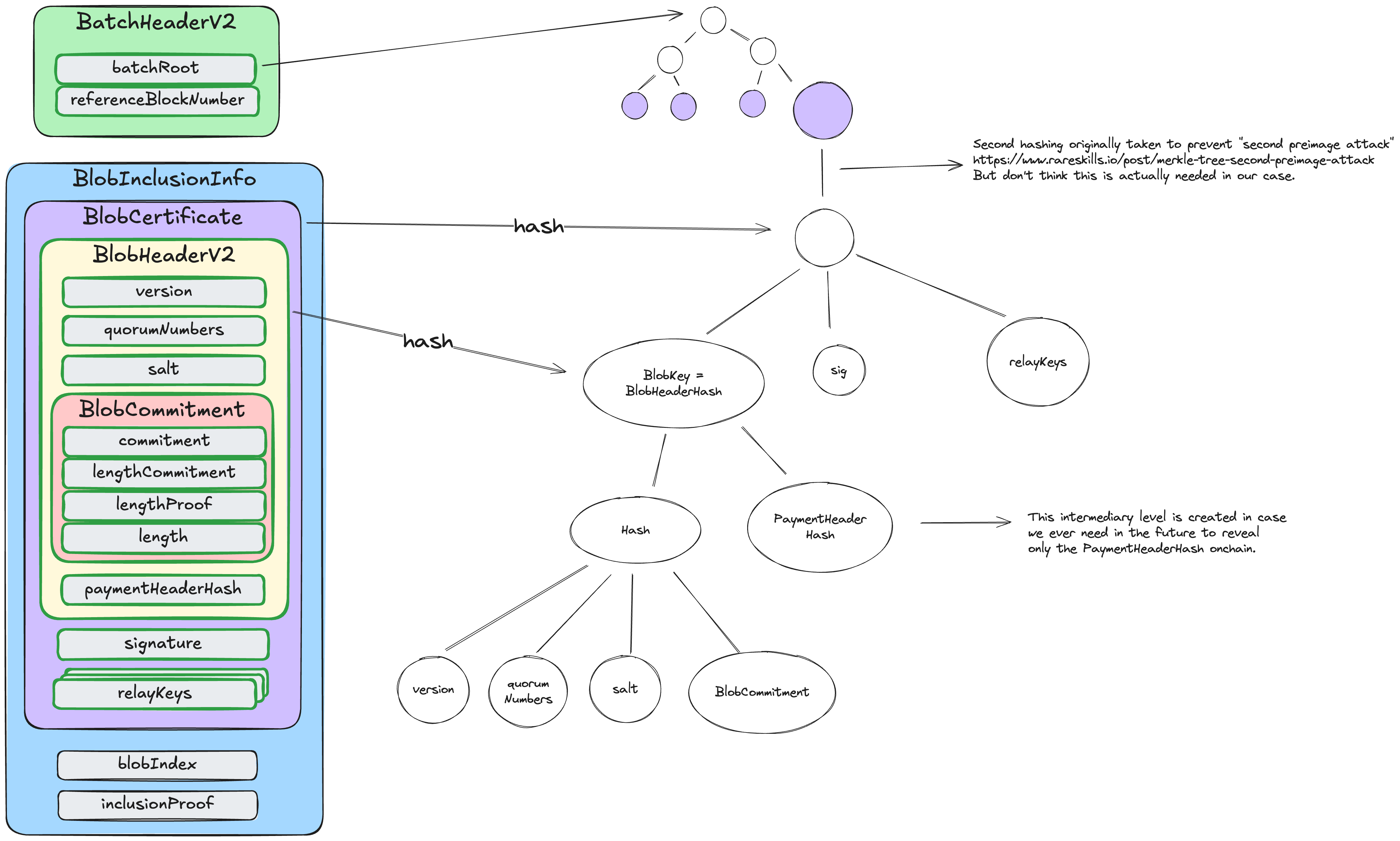
BlobKey (Blob Header Hash)
The blobKey (also known as blob_header_hash or blobHeaderHash) serves as the primary lookup key throughout the EigenDA system. It uniquely identifies a blob dispersal and is used for querying dispersal status, retrieving blobs from the network, and linking blobs to their certificates. The blobKey is computed as the keccak256 hash of the ABI-encoded BlobHeader, and is cryptographically equivalent to the blob_header_hash used in on-chain verification.
Computing the BlobKey
The hashing follows a nested structure. The inner hash covers the blob's content and dispersal requirements (version, quorums, commitment), which is then combined with the payment metadata hash. This ensures that each dispersal request produces a unique blobKey, even when dispersing identical blob content. The disperser enforces this uniqueness; attempting to disperse a blob with a previously used blobKey will result in rejection:
blobKey = keccak256(
abi.encode(
keccak256(abi.encode(blobHeader.version, blobHeader.quorumNumbers, blobHeader.commitment)),
blobHeader.paymentHeaderHash
)
)
Note: The paymentHeaderHash is the keccak256 hash of the PaymentHeader structure (described in the BlobHeader section above). The payment metadata is hashed separately to enable efficient on-chain verification while keeping payment details compact. Additionally, quorumNumbers are sorted in ascending order before hashing to ensure consistency regardless of the order in which quorums are specified.
When a rollup receives an encoded DA commitment from the proxy, the blobKey can be extracted by deserializing the BlobCertificate from the commitment payload, extracting its BlobHeader, and computing the hash as shown above.
In the standard dispersal flow, the disperser computes the blobKey and returns it to the client in the DisperseBlobReply. Clients may independently compute the blobKey for verification purposes or when extracting it from a certificate. The Go and Solidity implementations provided enable both client-side and on-chain computation.
Example
For illustrative purposes, consider a blob dispersal with the following parameters:
version:0x0001quorumNumbers:[0, 1](sorted)commitment: Cryptographic commitment to the blob data (G1 point and G2 length commitment)paymentHeaderHash:0x1234...(32-byte hash of the PaymentHeader)
The blobKey computation proceeds in two steps:
-
Compute inner hash of core dispersal parameters:
innerHash = keccak256(abi.encode(version, quorumNumbers, commitment))This produces a 32-byte hash representing the blob's content and dispersal requirements.
-
Compute outer hash combining inner hash with payment:
blobKey = keccak256(abi.encode(innerHash, paymentHeaderHash))This produces the final 32-byte
blobKey.
The resulting blobKey serves as the unique identifier for querying dispersal status with GetBlobStatus, retrieving chunks from validators via GetChunks, or fetching the full blob from relays via GetBlob.
Relationship to Other Data Structures
The BlobHeader is hashed to produce the blobKey. A BlobCertificate wraps a BlobHeader along with signature and relay keys. The BlobInclusionInfo contains a BlobCertificate and is used to prove inclusion of that certificate in a batch via a Merkle proof. The BatchHeader contains a batchRoot which is the root of the Merkle tree whose leaves are hashes of BlobCertificates. The diagram in the EigenDA Certificate section below illustrates these relationships.
Code References
The Solidity implementation can be found in hashBlobHeaderV2().
The Go implementation is available in ComputeBlobKey().
The EigenDA Go client demonstrates best practices for blobKey verification in verifyReceivedBlobKey(). After receiving a DisperseBlobReply, clients should verify that the disperser didn't modify the BlobHeader by computing the blobKey locally and comparing it with the returned value.
Usage
The blobKey is a central identifier used throughout the dispersal and retrieval process:
-
Dispersal phase: The disperser's
DisperseBlobmethod returns ablobKey. Clients then use thisblobKeywithGetBlobStatusto check when dispersal is complete (see Disperser polling). -
Centralized retrieval: The Relay API's
GetBlobmethod uses theblobKeyas its main lookup parameter to retrieve the full blob from relay servers (see Retrieval Paths). -
Decentralized retrieval: Validators'
GetChunksmethod uses theblobKeyto retrieve erasure-coded chunks directly from validator nodes. Clients can reconstruct the full blob from these chunks (see Retrieval Paths). -
Peripheral APIs: Both the Data API and the Blob Explorer rely on
blobKeyas the primary identifier for querying blob metadata and status. -
Verification: The
blobKeyconnects each blob to its certificate, ensuring that the certificate corresponds to the correct blob.
EigenDA Certificate (DACert)
An EigenDA Certificate (or short DACert) contains all the information needed to retrieve a blob from the EigenDA network, as well as validate it.
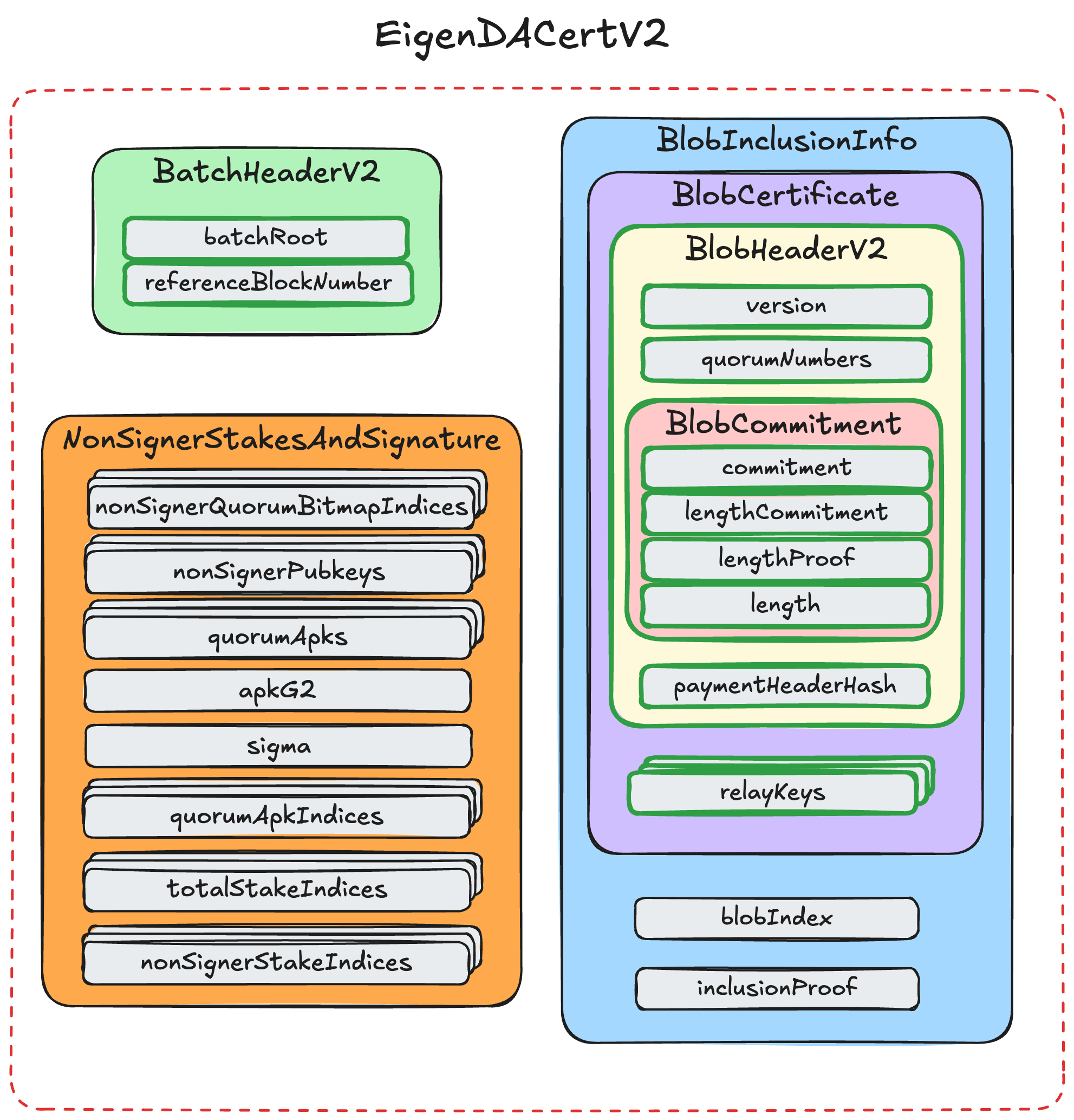
A DACert contains the four data structs needed to call checkDACert on the EigenDACertVerifier.sol contract. Please refer to the eigenda core spec for more details, but in short, the BlobCertificate is included as a leaf inside the merkle tree identified by the batch_root in the BatchHeader. The BlobInclusionInfo contains the information needed to prove this merkle tree inclusion. The NonSignerStakesAndSignature contains the aggregated BLS signature sigma of the EigenDA validators. sigma is a signature over the BatchHeader. The signedQuorumNumbers contains the quorum IDs that DA nodes signed over for the blob.
Cert Version
After the Blazer EigenDA network upgrade, three DACert versions exist: V2, V3, and V4. Integrations are expected to use the latest version.
- EigenDACertV2: The diagram displays all the members.
- EigenDACertV3: Defined in the contract. It contains the same members as EigenDACertV2, but with a different ordering:
BatchHeaderV2appears as the first member. - EigenDACertV4: Identical to EigenDACertV3 except for an additional uint16 field named offchainDerivationVersion, appended at the end. See contract.
AltDACommitment
In order to be understood by each rollup stack’s derivation pipeline, the encoded DACert must be prepended with header bytes, to turn it into an altda-commitment respective to each stack:
- op prepends 3 bytes:
version_byte,commitment_type,da_layer_byte - nitro prepends 1 byte:
version_byte
NOTE
In the future we plan to support a custom encoding byte which allows a user to specify different encoding formats for the DACert (e.g, RLP, ABI).