EigenDA
EigenDA is a Data Availability (DA) service, implemented as an actively validated service (AVS) on EigenLayer, that provides secure and scalable DA for L2s on Ethereum.
What is DA?
In informal terms, DA is a guarantee that a given piece of data will be available to anyone who wishes to retrieve it.
A DA system accepts blobs of data (via some interface) and then makes them available to retrievers (through another interface).
Two important aspects of a DA system are
- Security: The security of a DA system constitutes the set of conditions which are sufficient to ensure that all data blobs certified by the system as available are indeed available for honest retrievers to download.
- Throughput: The throughput of a DA system is the rate at which the system is able to accept blobs of data, typically measured in bytes/second.
An EigenLayer AVS for DA
EigenDA is implemented as an actively validated service on EigenLayer, which is a restaking protocol for Ethereum.
Because of this, EigenDA makes use of the EigenLayer state, which is stored on Ethereum, for consensus about the state of operators and as a callback for consensus about the availability of data. This means that EigenDA can be simpler in implementation than many existing DA solutions: EigenDA doesn't need to build it's own chain or consensus protocol; it rides on the back of Ethereum.
A first of its kind, horizontally scalable DA solution
Among extant DA solutions, EigenDA takes an approach to scalability which is unique in that it yields true horizontal scalability: Every additional unit of capacity contributed by an operator can increase the total system capacity.
This property is achieved by using a Reed Solomon erasure encoding scheme to shard the blob data across the DA nodes. While other systems such as Celestia and Danksharding (planned) also make use of Reed Solomon encoding, they do so only for the purpose of supporting certain observability properties of Data Availability Sampling (DAS) by light nodes. On the other hand, all incentivized/full nodes of the system download, store, and serve the full system bandwidth.
Horizontal scalability provides the promise for the technological bottlenecks of DA capacity to continually track demand, which has enormous implications for Layer 2 ecosystems.
Security Model
EigenDA produces a DA attestation which asserts that a given blob or collection of blobs is available. Attestations are anchored to one or more "Quorums," each of which defines a set of EigenLayer stakers which underwrite the security of the attestation. Quorums should be considered as redundant: Each quorum linked to an attestation provides an independent guarantee of availability as if the other quorums did not exist.
Each attestation is characterized by safety and liveness tolerances:
- Liveness tolerance: Conditions under which the system will produce an availability attestation.
- Safety tolerance: Conditions under which an availability attestation implies that data is indeed available.
EigenDA defines two properties of each blob attestation which relate to its liveness and safety tolerance:
- Liveness threshold: The liveness threshold defines the minimum percentage of stake which an attacker must control in order to mount a liveness attack on the system.
- Safety threshold: The safety threshold defines the total percentage of stake which an attacker must control in order to mount a first-order safety attack on the system.
The term "first-order attack" alludes to the fact that exceeding the safety threshold may represent only a contingency rather than an actual safety failure due to the presence of recovery mechanisms that would apply during such a contingency. Discussion of such mechanisms is outside of the scope of the current documentation.
Safety thresholds can translate directly into cryptoeconomic safety properties for quorums consisting of tokens which experience toxicity in the event of publicly observable attacks by a large coalition of token holders. This and other discussions of cryptoeconomic security are also beyond the scope of this technical documentation. We restrict the discussion to illustrating how the protocol preserves the given safety and liveness thresholds.
Glossary
Rollup Batcher
Sequencer rollup node component responsible for constructing and submitting to the settlement chain user transaction batches
Rollup Nodes
Refers to any rollup node (e,g, validator, verifier) which syncs current chain state through an onchain sequencer inbox.
EigenDA Proxy
Side car server as a part of rollup and used for secure and trustless communication with EigenDA.
EigenDA Client
A collection of clients used for securely dispersing and reading EigenDA blobs.
Rollup Payload
Compressed batches of transactions or state diffs.
DA Certificate (DACert)
An EigenDA Certificate (or DACert for short) contains all the information needed to retrieve a blob from the EigenDA network and validate it.
EigenDA Blob Derivation
A sequence of procedures to convert a byte array representing a DA certificate to the final rollup payload.
Preimage Oracle
An object with an interface for fetching additional data during EigenDA blob derivation by using some keys generated from the data. Multiple implementations of the preimage oracle show up in the EigenDA. In proxy, ETH rpc serves as the preimage oracle for DAcert validity; EigenDA network rpc serves as the preimage oracle for EigenDA blob.
Blob Field Element
EigenDA uses bn254 curve, a field element on the bn254 curve is an integer whose range is 0 <= x < 21888242871839275222246405745257275088548364400416034343698204186575808495617.
EigenDA Protocol
Broken down into 2 main sections.
Core Services
EigenDA Protocol consists of a suite of services that allow for data to be securely stored and retrieved from the validators.
Contracts
System Architecture
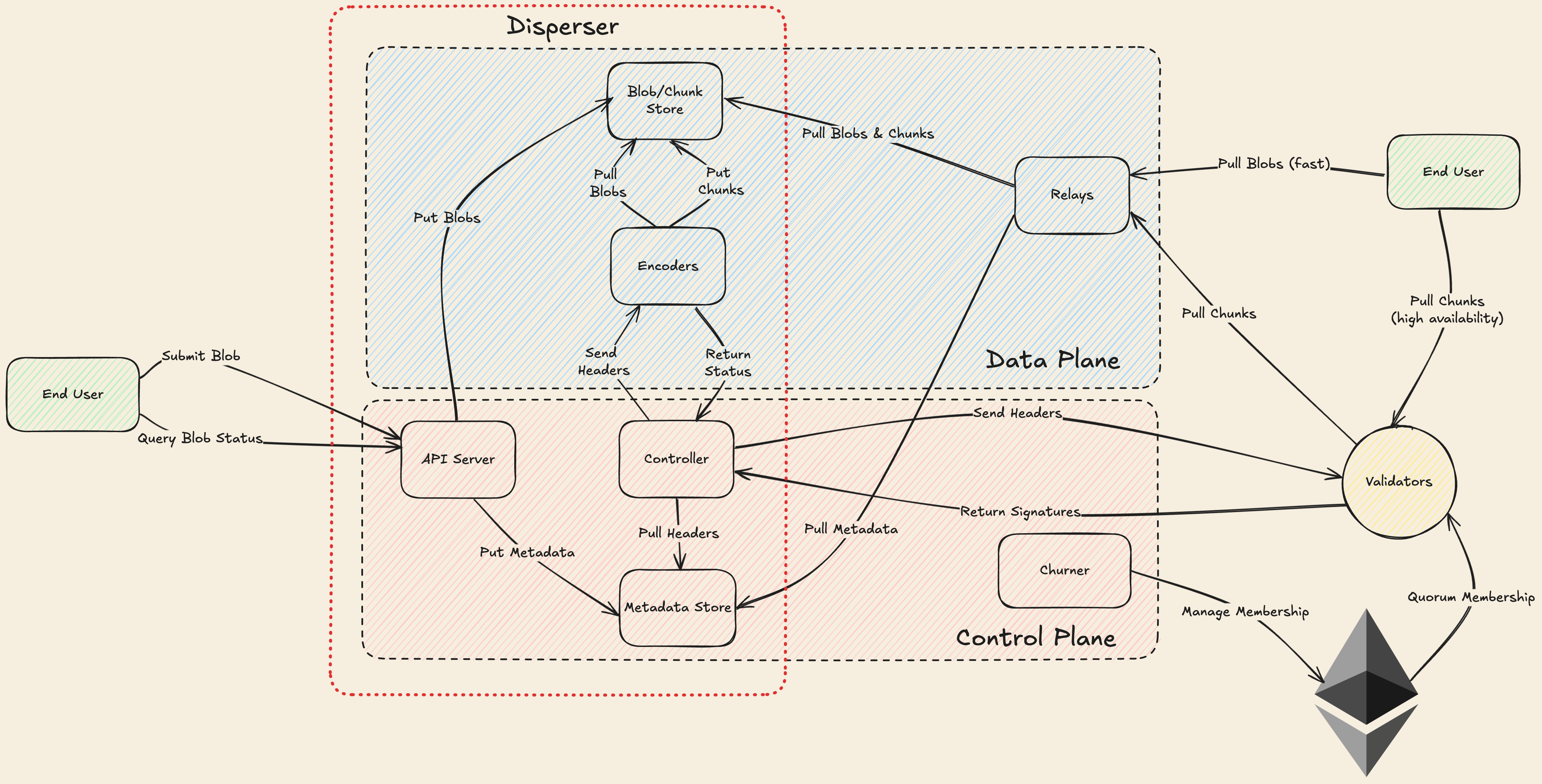
Core Components
- DA nodes are the service providers of EigenDA, storing chunks of blob data for a predefined time period and serving these chunks upon request.
- The disperser is responsible for encoding blobs, distributing them to the DA nodes, and aggregating their digital signatures into a DA attestation. As the disperser is currently centralized, it is trusted for system liveness; the disperser will be decentralized over time.
- The disperser and the DA nodes both depend on the Ethereum L1 for shared state about the DA node registration and stake delegation. The L1 is also currently used to bridge DA attestations to L2 end-user applications such as rollup chains.
Essential flows
Dispersal. The is the flow by which data is made available and consists of the following steps:
- The Disperser receives a collection of blobs, [encodes them], constructs a batch of encoded blobs and headers, and sends the sharded batch to the DA nodes.
- The DA nodes validate their shares of the batch, and return an attestation consisting of a BLS signature of the batch header.
- The disperser collects the attestations from the DA nodes and aggregates them into a single aggregate attestation.
Bridging. For a DA attestation to be consumed by the L2 end-user (e.g. a rollup), the it must be bridged to a chain from which the L2 can read. This might simply be the Ethereum L1 itself, but in many cases it is more economical to bridge directly into the L2 since this drastically decreases signature verification costs. For the time being all attestations are bridged to the L1 by the disperser.
Retrieval. Interested parties such as rollup challengers that want to obtain rollup blob data can retrieve a blob by downloading the encoded chunks from the DA nodes and decoding them. The blob lookup information contained in the request is obtained from the bridged attestation to the DA nodes.
Protocol Overview
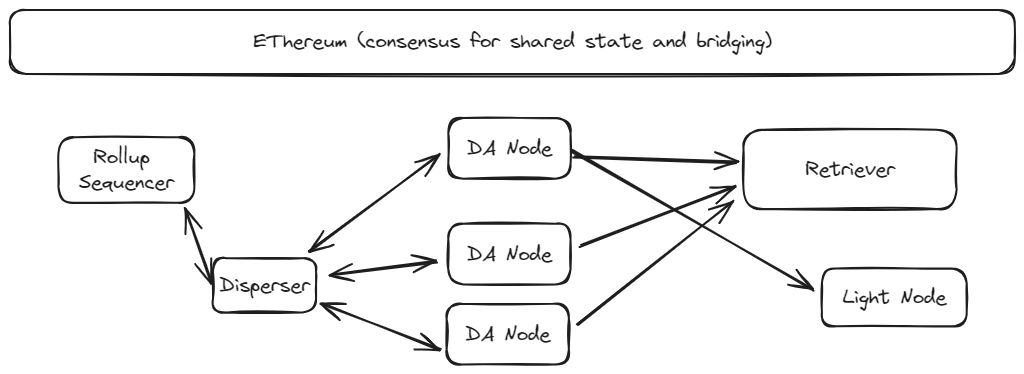
For expositional purposes, we will divide the protocol into two conceptual layers:
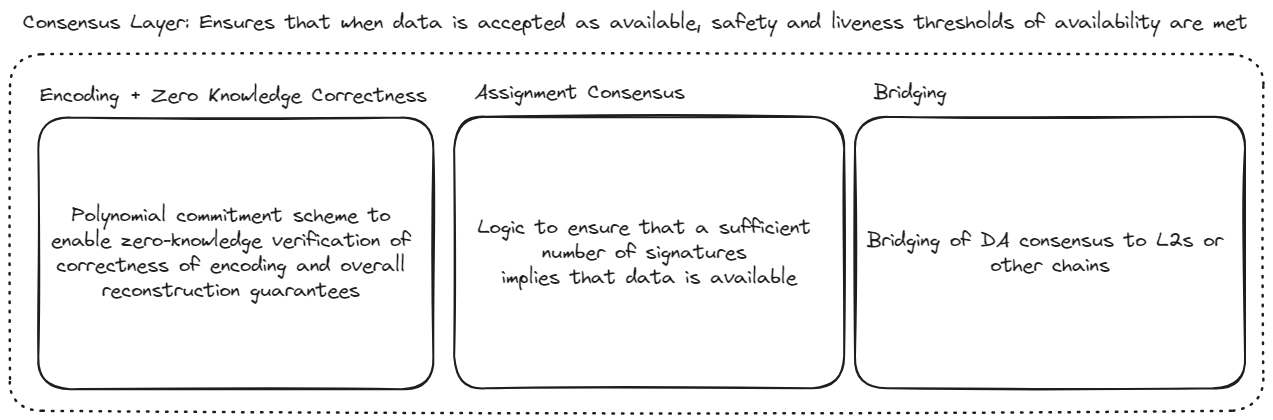
- Attestation Layer: Modules to ensure that whenever a DA attestation is accepted by an end-user (e.g. a rollup), then the data is indeed available. More specifically, the attestation layer ensures that the system observes the safety and liveness tolerances defined in the Security Model section.
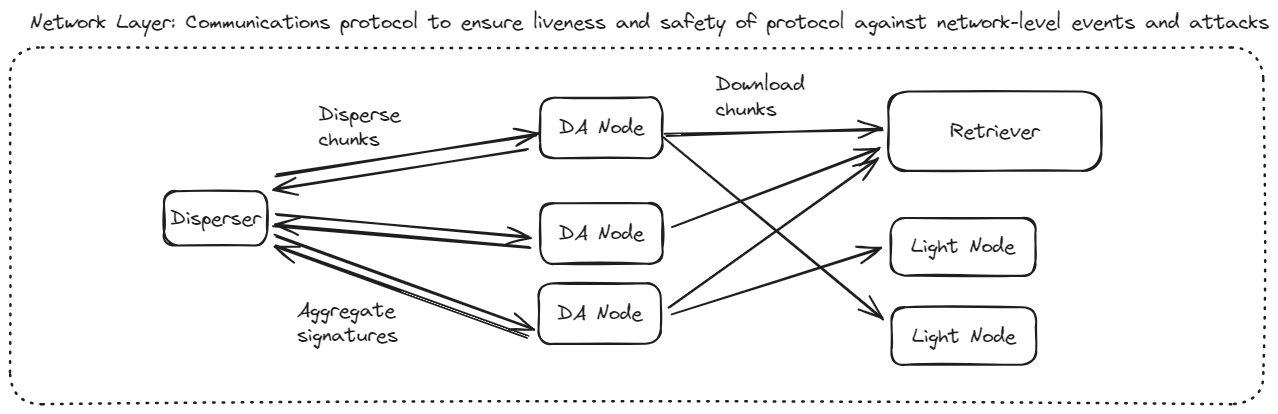
- Network Layer: The communications protocol which ensures that the liveness and safety of the protocol are robust against network-level events and threats.
Attestation Layer
The attest layer is responsible for ensuring that when the network-level assumptions and safety and liveness tolerances are observed, the system properly makes data available.
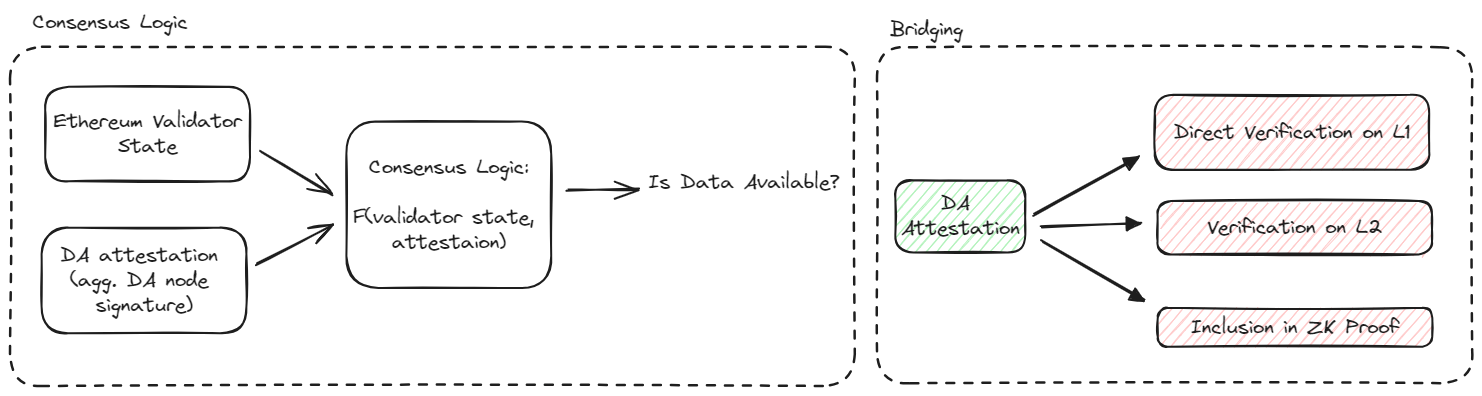
The primary responsibility of the attestation layer is to enable consensus about whether a given blob of data is fully within the custody of a set of honest nodes. (Here, what can be taken to be a set of honest nodes is defined by the system safety tolerance and the assurance that these honest nodes will be able to transmit the data to honest retrievers is handled by the network layer.) Since EigenDA is an EigenLayer AVS it does not need its own actual consensus protocol, but can instead piggy-back off of Ethereum's consensus. As a result, the attestation layer decomposes into two fairly straightforward pieces:
- Attestation Logic: The attestation logic allows us to answer the question of whether a given blob is available, given both a DA attestation and the validator state at the associated Ethereum block. The attestation logic can be understood as simply a function of these inputs which outputs yes or no, depending on whether these inputs imply that data is available. Naturally, this function is grounded upon assumptions about the behavior of honest nodes, which must perform certain validation actions as part of the attestation layer. The attestation logic further decomposes into two major modules:
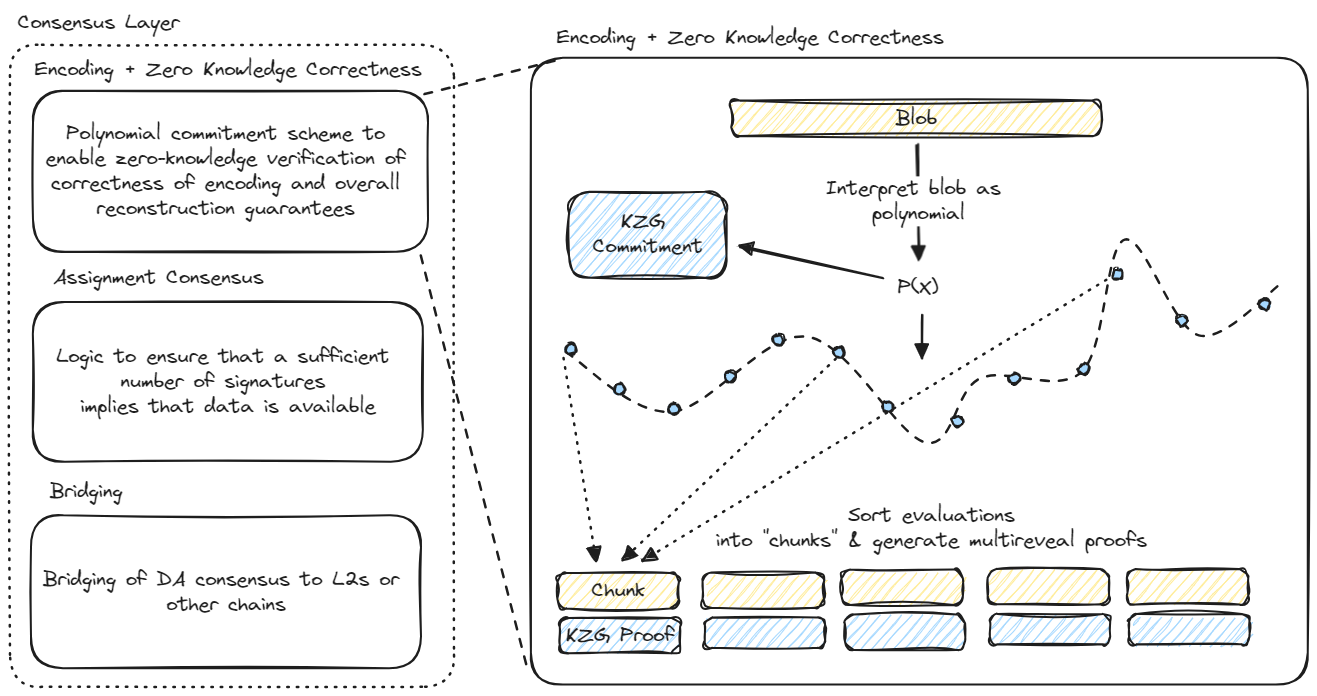
- Encoding: The encoding module defines a procedure for blobs to be encoded in such a way that their successful reconstruction can be guaranteed given a large enough collection of unique encoded chunks. The procedure also allows for the chunks to be trustlessly verified against a blob commitment so that the disperser cannot violate the protocol.
- Assignment: The assignment module provides a deterministic mapping from validator state to an allocation of encoded chunks to DA nodes. The mapping is designed to uphold safety and liveness properties with minimal data-inefficiency.
- Bridging: Bridging describes how the attestation is bridged to the consumer protocol, such as that of the rollup. In principle, bridging can be performed in one of several different ways in order to optimize efficiency and composability. At the moment, only bridging via the Ethereum L1 is directly supported.
The desired behavior of the attestation logic can be formally described as follows (Ignore this if you're happy with the high level ideas): Let \(\alpha\) denote the safety threshold, i.e. the maximum proportion of adversarial stake that the system is able to tolerate. Likewise, let \(\beta\) represent the amount of stake that we require to be held by the signing operators in order to accept an attestation, i.e. one minus the liveness threshold. Also, let \(O\) denote the set of EigenDA operators.
We need to guarantee that any set of signing operators \(U_q \subseteq O\) such that
and any set of adversarial operators such
we can reconstruct the original data blob from the chunks held by \( U_q \setminus U_a \).
Encoding Module
The encoding module defines a procedure for blobs to be encoded in such a way that their successful reconstruction can be guaranteed given a large enough collection of unique encoded chunks. The procedure also allows for the chunks to be trustlessly verified against a blob commitment so that the disperser cannot violate the protocol.
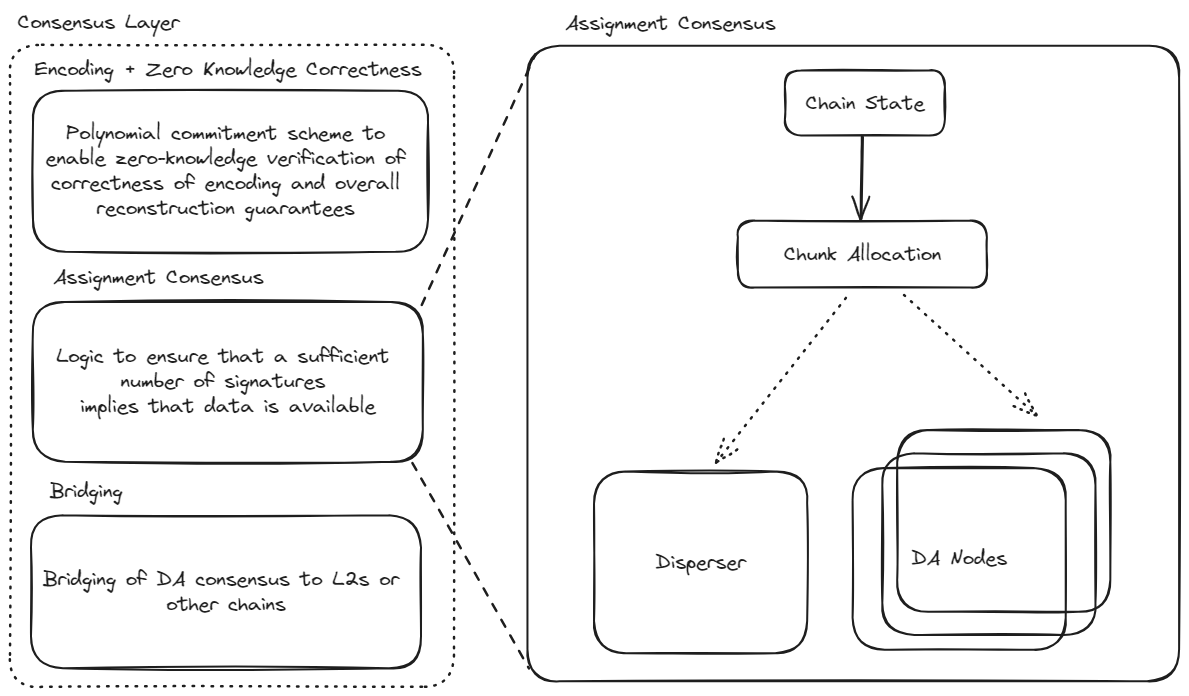
Assignment Module
The assignment module is nothing more than a rule which takes in the Ethereum chain state and outputs an allocation of chunks to DA operators.
Signature verification and bridging
See the integration contracts section for details on how the attestation is bridged to the consumer protocol, such as that of the rollup.
Network Layer
The network layer is described in the Write and Read Workflow, which explains how each component interacts when writing to and reading from EigenDA.
Encoding Module
The encoding module defines a procedure for blobs to be encoded in such a way that their successful reconstruction can be guaranteed given a large enough collection of unique encoded chunks. The procedure also allows for the chunks to be trustlessly verified against a blob commitment so that the disperser cannot violate the protocol.
One way to think of the encoding module is that it must satisfy the following security requirements:
- Adversarial tolerance for DA nodes: We need to have tolerance to arbitrary adversarial behavior by any number of DA nodes up to some threshold. Note that while simple sharding approaches such as duplicating slices of the blob data have good tolerance to random node dropout, they have poor tolerance to worst-case adversarial behavior.
- Adversarial tolerance for disperser: We do not want to put trust assumptions on the encoder or rely on fraud proofs to detect if an encoding is done incorrectly.
Trustless Encoding via KZG and Reed-Solomon
EigenDA uses a combination of Reed-Solomon (RS) erasure coding and KZG polynomial commitments to perform trustless encoding. In this section, we provide a high level overview of how the EigenDA encoding module works and how it achieves these properties.
Reed Solomon Encoding
Basic RS encoding is used to achieve the first requirement of Adversarial tolerance for DA nodes. This looks like the following:
- The blob data is represented as a string of symbols, where each symbol is elements in a certain finite field. The number of symbols is called the
BlobLength - These symbols are interpreted as the coefficients of a
BlobLength-1 degree polynomial. - This polynomial is evaluated at
NumChunks*ChunkLengthdistinct indices. - Chunks are constructed, where each chunk consists of the polynomial evaluations at
ChunkLengthdistinct indices.
Notice that given any number of chunks such that ChunkLength >= BlobLength, via polynomial interpolation it is possible to reconstruct the original polynomial, and therefore its coefficients which represent the original blob.
Validation via KZG
To address the requirement Adversarial tolerance for disperser using RS encoding alone requires fraud proofs: a challenger must download all of the encoded chunks and check that they lie on a polynomial corresponding to the blob commitment.
To avoid the need for fraud proofs, EigenDA follows the trail blazed by the Ethereum DA sharding roadmap in using KZG polynomial commitments.
Chunk Validation
Blobs sent to EigenDA are identified by their KZG commitment (which can be calculated by the disperser and easily validated by the rollup sequencer). When the disperser generates the encoded blob chunks, it also generates a collection of opening proofs which the DA nodes can use to trustlessly verify that their chunks fall on the blob polynomial at the correct indices (note: the indices are jointly derived by the disperser and DA nodes from the chain state using the logic in the Assignment module to ensure that the evaluation indices for each node are unique).
Blob Size Verification KZG commitments also can be used to verify the degree of the original polynomial, which in turn corresponds to the size of the original blob. Having a trustlessly verifiable upper bound on the size of the blob is necessary for DA nodes to verify the correctness of the chunk assignment defined by the assignment module.
The KZG commitment relies on a structured reference string (SRS) containing a generator point multiplied by all of the powers of some secret field element , up to some maximum power . This means that it is not possible to use this SRS to commit to a polynomial of degree greater than . A consequence of this is that if is a polynomial of degree greater than , it will not be possible to commit to the polynomial . A "valid" commitment to the polynomial thus constitutes a proof that the polynomial is of degree less than or equal to .
In practice, this looks like the following:
- If the disperser wishes to claim that the polynomial is of degree less than or equal to , they must provide along with the commitment to , a commitment to .
- The verifier then performs the pairing check , where is the G2 generator and is the 'th power of tau. This pairing will only evaluate correctly when was constructed as described above and .
Note: The blob length verification here allows for the blob length to be upper-bounded; it cannot be used to prove the exact blob length.
Prover Optimizations
EigenDA makes use of the results of Fast Amortized Kate Proofs, developed for Ethereum's sharding roadmap, to reduce the computational complexity for proof generation.
See the full discussion
Verifier Optimizations
Without any optimizations, the KZG verification complexity can lead to a computational bottleneck for the DA nodes. Fortunately, the Universal Verification Equation developed for Danksharding data availability sampling dramatically reduces the complexity. EigenDA has implemented this optimization to eliminate this bottleneck for the DA nodes.
Amortized KZG Prover Backend
It is important that the encoding and commitment tasks are able to be performed in seconds and that the dominating complexity of the computation is nearly linear in the degree of the polynomial. This is done using algorithms based on the Fast Fourier Transform (FFT).
This document describes how the KZG-FFT encoder backend implements the Encode(data [][]byte, params EncodingParams) (BlobCommitments, []*Chunk, error) interface, which 1) transforms the blob into a list of params.NumChunks Chunks, where each chunk is of length params.ChunkLength 2) produces the associated polynomial commitments and proofs.
We will also highlight the additional constraints on the Encoding interface which arise from the KZG-FFT encoder backend.
Deriving the polynomial coefficients and commitment
As described in the Encoding Module Specification, given a blob of data, we convert the blob to a polynomial by simply slicing the data into a string of symbols, and interpreting this list of symbols as the tuple .
In the case of the KZG-FFT encoder, the polynomial lives on the field associated with the BN254 elliptic curve, which as order [TODO: fill in order].
Given this polynomial representation, the KZG commitment can be calculated as in KZG polynomial commitments.
Polynomial Evaluation with the FFT
In order to use a Discrete Fourier Transform (DFT) to evaluate a polynomial, the indices of the polynomial evaluations which will make up the Chunks must be members of a cyclic group, which we will call . A cyclic group is the group generated by taking all of the integer powers of some generator , i.e., (For this reason, the elements of a cyclic group of order will sometimes be referred to as the ’th roots of unity). Notice that since our polynomial lives on the BN254 field, the group must be a subgroup of that field (i.e. all of its elements must lie within that field).
Given a cyclic group of order , we can evaluate a polynomial of order at the indices contained in via the DFT,
where gives the evaluation of the polynomial at . Letting denote the vector of polynomial coefficients and the vector of polynomial evaluations, we can use the shorthand . The inverse relation also holds, i.e., .
To evaluate the DFT programmatically, we want . Notice that we can achieve this when by simply padding with zeros to be of length .
The use of the FFT can levy an additional requirement on the size of the group . In our implementation, we require the size of to be a power of 2. For this, we can make use of the fact that the prime field associated with BN254 contains a subgroup of order , which in turn contains subgroups of orders spanning every power of 2 less than .
As the encoding interface calls for the construction of NumChunks Chunks of length ChunkLength, our application requires that be of size NumChunks*ChunkLength, which in turn must be a power of 2.
Amortized Multireveal Proof Generation with the FFT
The construction of the multireveal proofs can also be performed using a DFT (as in “Fast Amortized Kate Proofs”). Leaving the full details of this process to the referenced document, we describe here only 1) the index-assignment the scheme used by the amortized multiproof generation approach and 2) the constraints that this creates for the overall encoder interface.
Given the group corresponding to the indices of the polynomial evaluations and a cyclic group which is a subgroup of , the cosets of in are given by
Each coset has size , and there are unique and disjoint cosets.
Given a polynomial and the groups and , the Amortized Kate Proofs approach generates different KZG multi-reveal proofs, where each proof is associated with the evaluation of at the indices contained in a single coset for . Because the Amortized Kate Proofs approach uses the FFT under the hood, itself must have an order which is a power of 2.
For the purposes of the KZG-FFT encoder, this means that we must choose to be of size NumChunks*ChunkLength and to be of size ChunkLength, each of which must be powers of 2.
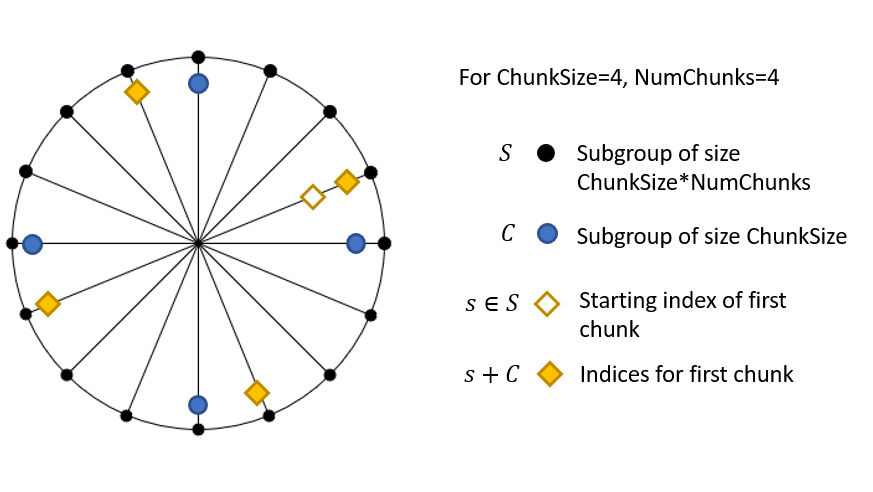
Worked Example
As a simple illustrative example, suppose that AssignmentCoordinator provides the following parameters in order to meet the security requirements of a given blob:
ChunkLength= 3NumChunks= 4
Supplied with these parameters, Encoder.ParamsFromMins will upgrade ChunkLength to the next highest power of 2, i.e., ChunkLength = 4, and leave NumChunks unchanged. The following figure illustrates how the indices will be assigned across the chunks in this scenario.
Assignment Module
The assignment module determines how encoded blob chunks are allocated to validators based on the Ethereum chain state, specifically validator stakes and quorum memberships. Given the validator state and blob parameters, it produces a deterministic mapping from validators to chunk indices. The mapping ensures that a sufficient number of signatures and honest validators implies that data is available.
The assignment module is implemented in core/v2/assignment.go. For blobs dispersed to multiple quorums, the algorithm employs overlap optimization to minimize storage requirements while maintaining security guarantees.
Chunk Assignment Algorithm within One Quorum
The chunk assignment scheme assigns encoded chunks to validators proportionally to their stake, ensuring that any coalition of validators with sufficient combined stake can reconstruct the blob.
Given:
- A set of validators with stakes , where
- A set of chunks to be assigned to the validators
Within a single quorum, the number of chunks assigned to validator is:
c_i = \lceil \eta_i(c - n) \rceil
This assignment ensures that the total number of assigned chunks is less than or equal to the total number of chunks , since .
This guarantees that the chunks assigned to validators within a quorum are non-overlapping. In other words, each validator in a quorum contributes distinct chunks for reconstruction. The proof that any subset of validators with sufficient combined stake can reconstruct the blob is provided in Security Parameters.
Chunk Assignment for Multiple Quorums
EigenDA supports blobs dispersed to multiple quorums simultaneously. The security threshold is guaranteed to hold for each quorum independently, as shown in the previous section. The multi-quorum assignment algorithm minimizes storage requirements through overlap optimization while maintaining security guarantees.
Storage Optimization Strategy
The assignment algorithm uses two key strategies to minimize storage:
-
Chunk Overlap Maximization: When a validator participates in multiple quorums for the same blob, the algorithm reuses the same chunk indices across quorums whenever possible.
-
Reconstruction Capping: Each validator is assigned at most the number of chunks needed to independently reconstruct the blob.
Example: Consider a validator with 5% stake in quorum 0 and 15% stake in quorum 1. Without optimization, the validator might receive two non-overlapping sets of chunks (one per quorum), totaling up to 20% of all chunks. With overlap optimization, the validator stores only max(chunks_quorum_0, chunks_quorum_1) unique chunks, which is 15% of the total chunks. With reconstruction capping, if the coding rate is , the validator only needs to store 1/8 of the total chunks.
Algorithm Components
The multi-quorum assignment algorithm consists of four key functions:
1. GetAssignmentsForQuorum: Calculates assignments for a single quorum independently using the stake-proportional algorithm described above.
2. AddAssignmentsForQuorum: Generates the assignment for a new quorum while maximizing overlap with a baseline quorum assignment through a two-phase process:
-
Phase 1 (Overlap Maximization): For each validator, reuse as many chunk indices as possible from the baseline quorum assignment, up to the number required for the new quorum. Mark these reused indices as "used."
-
Phase 2 (Gap Filling): Distribute the remaining unused chunk indices to validators who need additional chunks beyond what was reused from the baseline, ensuring each validator receives their stake-proportional allocation in the new quorum.
This algorithm guarantees that validators participating in both quorums store only max(chunks_in_quorum_1, chunks_in_quorum_2) unique chunks rather than the sum.
3. MergeAssignmentsAndCap: Merges assignments across all quorums and caps the total at the reconstruction threshold:
\text{max\_chunks} = c \cdot \gamma
where is the total number of chunks and is the coding rate. This cap exists because once a validator has enough unique chunks to reconstruct the blob, additional chunks provide no incremental security benefit. Therefore, pruning the extra chunks improves performance and reduces storage and bandwidth requirements without affecting security.
4. GetAssignmentsForBlob: Coordinates the full multi-quorum assignment process:
- Generate the assignment for quorum 0 using
GetAssignmentsForQuorum - Generate assignments for all other quorums using
AddAssignmentsForQuorumwith quorum 0 as the baseline - Merge all per-quorum assignments using
MergeAssignmentsAndCapto produce the final assignment for each validator
Note on Optimality: The algorithm produces optimal storage assignments for two quorums. For three or more quorums, the assignment is not guaranteed to be globally optimal. Since quorums 0 and 1 are the "default" quorums and are expected to be the larger than custom quorums (i.e. containing the most validators), the algorithm achieves near-optimal storage reduction for the majority of validators.
Code Walkthrough
Notation note: In the code, we sometimes use the term operator to refer to a validator, although validator is now the preferred term.
Location: core/v2/assignment.go
Data Structure:
type Assignment struct {
Indices []uint32 // Explicit list of chunk indices (non-contiguous)
}
Core Functions:
1. GetAssignmentsForQuorum (core/v2/assignment.go:40-90)
Assigns chunks for a single quorum with deterministic ordering:
func GetAssignmentsForQuorum(
state *core.OperatorState,
blobParams *core.BlobVersionParameters,
quorum core.QuorumID,
) (map[core.OperatorID]*Assignment, []core.OperatorID, error)
Algorithm:
- Sort operators by hex ID for determinism
- Calculate effective chunks:
effectiveNumChunks = NumChunks - MaxNumOperators - For each operator :
chunksForOperator = ceil((effectiveNumChunks × stake_i) / totalStake) - Assign contiguous indices starting from offset 0
- Return assignments and ordered operator list
2. AddAssignmentsForQuorum (core/v2/assignment.go:99-161)
Maximizes overlap with a baseline assignment:
func AddAssignmentsForQuorum(
assignments map[core.OperatorID]*Assignment, // Baseline from first quorum
state *core.OperatorState,
blobParams *core.BlobVersionParameters,
quorum core.QuorumID,
) (map[core.OperatorID]*Assignment, error)
Two-phase algorithm:
- Phase 1 (Lines 115-136): For each operator, reuse indices from baseline up to their allotted count for this quorum
- Phase 2 (Lines 145-158): Distribute unused indices to operators needing more chunks
3. MergeAssignmentsAndCap (core/v2/assignment.go:167-220)
func MergeAssignmentsAndCap(
assignments []map[core.OperatorID]*Assignment,
blobParams *core.BlobVersionParameters,
) map[core.OperatorID]Assignment
Merges all quorum assignments and caps at maxChunks = NumChunks / CodingRate
4. GetAssignmentsForBlob (core/v2/assignment.go:227-266)
Main entry point coordinating the full multi-quorum assignment:
func GetAssignmentsForBlob(
state *core.OperatorState,
blobParams *core.BlobVersionParameters,
quorums []core.QuorumID,
) (map[core.OperatorID]Assignment, error) {
// Sort quorums for determinism
sort.Slice(quorums, ...)
// Process first quorum
assignmentsList[0], _, err = GetAssignmentsForQuorum(state, blobParams, quorums[0])
// Process remaining quorums with overlap optimization
for i := 1; i < len(quorums); i++ {
assignmentsList[i], err = AddAssignmentsForQuorum(
assignmentsList[0], state, blobParams, quorums[i])
}
// Merge and cap
return MergeAssignmentsAndCap(assignmentsList, blobParams)
}
Usage in Node Chunk Download (node/node_v2.go:40-105):
func (n *Node) DetermineChunkLocations(
batch *corev2.Batch,
operatorState *core.OperatorState,
) {
for _, cert := range batch.BlobCertificates {
// Get assignment for this operator across ALL quorums in the blob
assgn, err := corev2.GetAssignmentForBlob(
operatorState,
blobParams,
cert.BlobHeader.QuorumNumbers, // Multiple quorums
n.Config.ID)
// Request specific chunk indices from relay
req.chunkRequests = append(req.chunkRequests, &relay.ChunkRequestByIndex{
BlobKey: blobKey,
Indices: assgn.Indices, // Explicit indices with overlap optimization
})
}
}
Usage in Validation (core/v2/validator.go:49-79):
func (v *shardValidator) validateBlobParams(
blob *BlobShard,
blobParams *core.BlobVersionParameters,
operatorState *core.OperatorState,
) (*Assignment, error) {
// Get assignment across all quorums for this blob
assignment, err := GetAssignmentForBlob(
operatorState,
blobParams,
blob.BlobHeader.QuorumNumbers, // All quorums
v.operatorID)
// Validate chunk count
if assignment.NumChunks() != uint32(len(blob.Bundle)) {
return error
}
// Validate chunk lengths
for _, chunk := range blob.Bundle {
if chunk.Length() != expectedChunkLength {
return error
}
}
return &assignment, nil
}
Security Parameters
This page proves the relationship between blob parameters and security thresholds. We also point readers to the code where security threshold constraints are implemented.
Blob Parameters and Reconstruction Threshold
In this part, we present the blob parameters and use these parameters to derive the reconstricution threshold.
Blob Parameters
We define the Blob parameters as a tuple where:
- (
MaxNumOperators): Maximum number of validators allowed in EigenDA. - (
NumChunks): The total number of encoded chunks after erasure coding (must be a power of 2). - (
1/CodingRate): The ratio of original data to total encoded chunks, providing redundancy (must be an inverse power of 2). Note that for representational purposes, theCodingRatein our code is the inverse of , while is the the standard coding rate used in coding theory.
Among the blob parameters, CodingRate and NumChunks are used in the encoding process, while NumChunks and MaxNumOperators are used in the chunk assignment process.
This tuple is stored in the struct shown below (see in the code):
struct VersionedBlobParams {
uint32 maxNumOperators;
uint32 numChunks;
uint8 codingRate;
}
The blob parameters for each version is stored in the EigenDAThresholdRegistry contract.
It's configured here and the default parameters are shown below.
versionedBlobParams = [
{ 0_maxNumOperators = 3537, 1_numChunks = 8192, 2_codingRate = 8 }
]
Note on MaxNumOperators
The MaxNumOperators parameter (n = 3537) serves as an upper bound used in the chunk assignment algorithm and security threshold derivations. This upper bound ensures that the reconstruction threshold and other security properties remain fixed and predictable, regardless of how many validators actually register.
The actual number of validators allowed to register for each quorum is controlled separately by the on-chain maxOperatorCount parameter in the OperatorSetParam struct. The current on-chain limits per quorum are:
- Quorum 0 (ETH): 200 validators
- Quorum 1 (EIGEN): 200 validators
- Quorum 2 (Custom): 15 validators
The per-quorum limits can be adjusted via governance without requiring changes to the blob parameters or security thresholds, as long as they remain below the upper bound.
For more details on how maxOperatorCount is enforced during operator registration, see the EigenDARegistryCoordinator
contract.
Reconstruction Threshold
We define ReconstructionThreshold, also denoted as , the minimum fraction of total stake required to reconstruct the blob.
In this section, we prove that, with our chunk assignment algorithm, the reconstruction threshold is:
, where .
In other words, we want to prove that any subset of validators with of total stake collectively own enough chunks to reconstruct the original blob.
Formally, we need to show that for any set of validators with total stake , the chunks assigned to satisfy .
Proof:
By the chunk assignment scheme, we have:
Therefore, since , we have:
Now, we prove that any subset of validators with of the total stake own at least chunks, which is guaranteed to reconstruct the origianl blob due to the property of Reed-Solomon encoding.
As we show in the previous subsection, by default, , and , which gives us the reconstruction threshold .
Intuition: Loss in Chunk Assignment
If we look closely at the reconstruction threshold, we find that it is given by the encoding rate multiplied by a factor:
This means that in practice, a group of validators needs to hold more stake than the theoretical threshold to guarantee reconstruction.
In an ideal world, any subset of validators holding a fraction of the total stake would also hold of the chunks, and therefore could recover the blob. But in reality, because chunk assignments are discrete, some loss occurs: a validator’s assigned share of chunks can be less than its stake share.
Suppose there are 10 chunks and 3 validators, each with one-third of the stake. Using the assignment algorithm, we might get:
- Validator 1 → 4 chunks
- Validator 2 → 3 chunks
- Validator 3 → 3 chunks
Here, Validator 2 has 33% of the stake but only 30% of the chunks. This loss can make the difference in meeting the reconstruction threshold.
The mismatch becomes even more pronounced as the number of validators increases.
Imagine 10 million validators, each with equal stake, but only 10,000 chunks to be assigned in total. In this case, only a small fraction of validators can get at least 1 chunk, while the majority get none at all. The loss is enormous.
This is why the MaxNumOperators becomes an important parameter in determining the reconstruction threshold: the more validators there are relative to the number of chunks, the higher the loss from assignment imbalance.
BFT Security
Having established the relationship between the blob parameters and the reconstruction threshold, we now turn to the Byzantine Fault Tolerant (BFT) security model and how it relates to the blob parameters.
Definition of Security Thresholds
In this section, we define and prove the safety and liveness properties of EigenDA, building on the reconstruction property established above.
The Byzantine liveness and safety properties of a blob are specified by a collection of SecurityThresholds:
ConfirmationThreshold- The confirmation threshold defines the minimum percentage of stake that must sign to make the DA certificate valid.SafetyThreshold- The safety threshold refers to the minimum percentage of total stake an attacker must control to make a blob with a valid DA certificate unavailable.LivenessThreshold- The liveness threshold refers to the minimum percentage of total stake an attacker must control to cause a liveness failure.
How to Set the Confirmation Threshold
In the BFT security model, the SafetyThreshold and LivenessThreshold are estimated by the client. The SafetyThreshold is the maximum stake controlled by an adversary that signs the certificate but fails to serve the data, while the LivenessThreshold is the maximum stake controlled by an adversary that does not sign the certificates.
The ConfirmationThreshold is set based on the following two criteria:
1. Confirmation Threshold and Safety Threshold
To ensure that each blob with a valid DA certificate is available, the following inequality must be satisfied when setting the ConfirmationThreshold:
ConfirmationThreshold - SafetyThreshold >= ReconstructionThreshold (1)
Intuitively, since the adversary controls less than SafetyThreshold of stake, at least ConfirmationThreshold - SafetyThreshold honest validators need to sign to form a valid DA certificate.
Therefore, as long as ConfirmationThreshold - SafetyThreshold >= ReconstructionThreshold, the honest validators should own a large enough set of chunks to reconstruct the blob.
⚠️
We strongly recommend that users set a SafetyThreshold >= 33% if they ever want to change the default settings.
2. Confirmation Threshold and Liveness Threshold
The ConfirmationThreshold and LivenessThreshold satisfy the following inequality:
ConfirmationThreshold <= 1 - LivenessThreshold (2)
This is because a valid certificate requires signatures from at least ConfirmationThreshold of stake. If ConfirmationThreshold is greater than 1 - LivenessThreshold, the adversary can cause a liveness failure by simply not signing the certificate.
In summary, the SafetyThreshold and LivenessThreshold depends on the choice of ConfirmationThreshold. The picture below shows the relationship between these security thresholds.
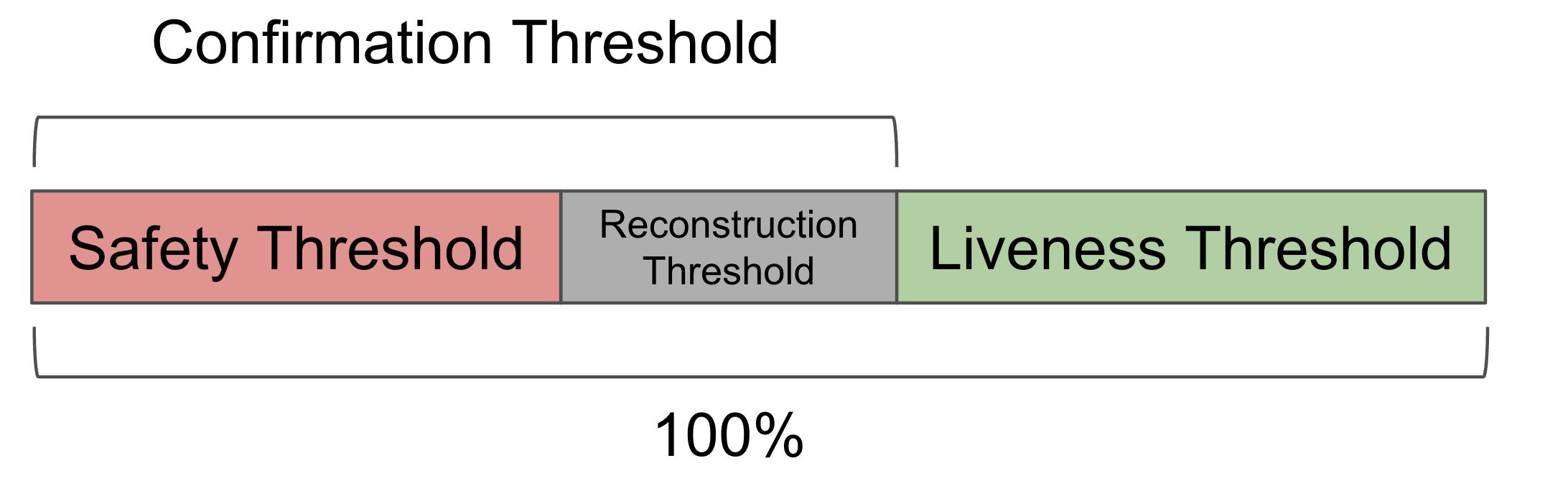
A table of the security thresholds is given below for the reader's reference, assuming that the reconstruction threshold is 22%.
| Confirmation Threshold | Safety Threshold | Liveness Threshold |
|---|---|---|
| 55% | 33% | 45% |
| 60% | 38% | 40% |
| 65% | 43% | 35% |
Implementation Details
In our code, we use slightly different names for the security thresholds compared to the notation in this document.
Here is the mapping from the notations in this doc to the variable names in the code:
ConfirmationThreshold→securityThresholds.confirmationThreshold(in percent)SafetyThreshold→securityThresholds.adversaryThreshold(in percent)- →
blobParams.numChunks - →
blobParams.maxNumOperators - → 1 /
blobParams.codingRate
Note that SafetyThreshold is called adversaryThreshold in the code.
Also, securityThresholds.confirmationThreshold and securityThresholds.adversaryThreshold are expressed in percent where the stored integer equals the required percentage.
For example, securityThresholds.confirmationThreshold = 55 means ConfirmationThreshold = 55%.
1. Safety Threshold
The check for the inequality (1) above is implemented as follows (see in code).
// Check for potential underflow: maxNumOperators must not exceed numChunks
if (blobParams.maxNumOperators > blobParams.numChunks) {
revert SecurityAssumptionsNotMet(
...
);
}
uint256 lhs = blobParams.codingRate * (blobParams.numChunks - blobParams.maxNumOperators) * (securityThresholds.confirmationThreshold - securityThresholds.adversaryThreshold);
uint256 rhs = 100 * blobParams.numChunks;
if (!(lhs >= rhs)) {
revert SecurityAssumptionsNotMet(
...
);
}
First, the code confirms that the total number of chunks is greater than the total number of validators so that ReconstructionThreshold is meaningful. Next, it validates the following inequality:
blobParams.codingRate * (blobParams.numChunks - blobParams.maxNumOperators) * (securityThresholds.confirmationThreshold - securityThresholds.adversaryThreshold) >= 100 * blobParams.numChunks
The inequality above can be be rewritten as:
(blobParams.numChunks - blobParams.maxNumOperators) / 100 >= blobParams.numChunks / (blobParams.codingRate * (blobParams.numChunks - blobParams.maxNumOperators))
By substituting the variables using the notation mapping shown at the beginning of this section and simplifying, we get:
(ConfirmationThreshold - SafetyThreshold) >= (c / (c - n)) * γ.
Recall that ReconstructionThreshold = (c / (c - n)) * γ, (c > n)(see more details in Reconstruction Threshold).
Therefore, the inequality above is exactly inequality (1) shown in the previous subsection.
2. Liveness Threshold
The LivenessThreshold does not appear in the code, but users should keep the equation (2) in mind when setting the confirmation ConfirmationThreshold.
System Default
The security threshods are configured as follows (see in the code):
{
"eigenDAServiceManager": "0x3a5acf46ba6890B8536420F4900AC9BC45Df4764",
"eigenDAThresholdRegistry": "0x0DA66C1930Acc54809093Bb42f2e6a4bE21d5403",
"defaultSecurityThresholds": {
"0_confirmationThreshold": 55,
"1_adversaryThreshold": 33
},
"quorumNumbersRequired": "0x0001"
}
By default, the ConfirmationThreshold is 55%. With the default ReconstructionThreshold = 22%, the default ConfirmationThreshold gives a SafetyThreshold of 33% and a LivenessThreshold of 45%.
Write and Read Workflow
This page provides an overview of the workflow for writing data to and reading data from EigenDA. The workflow is illustrated in the diagram below.
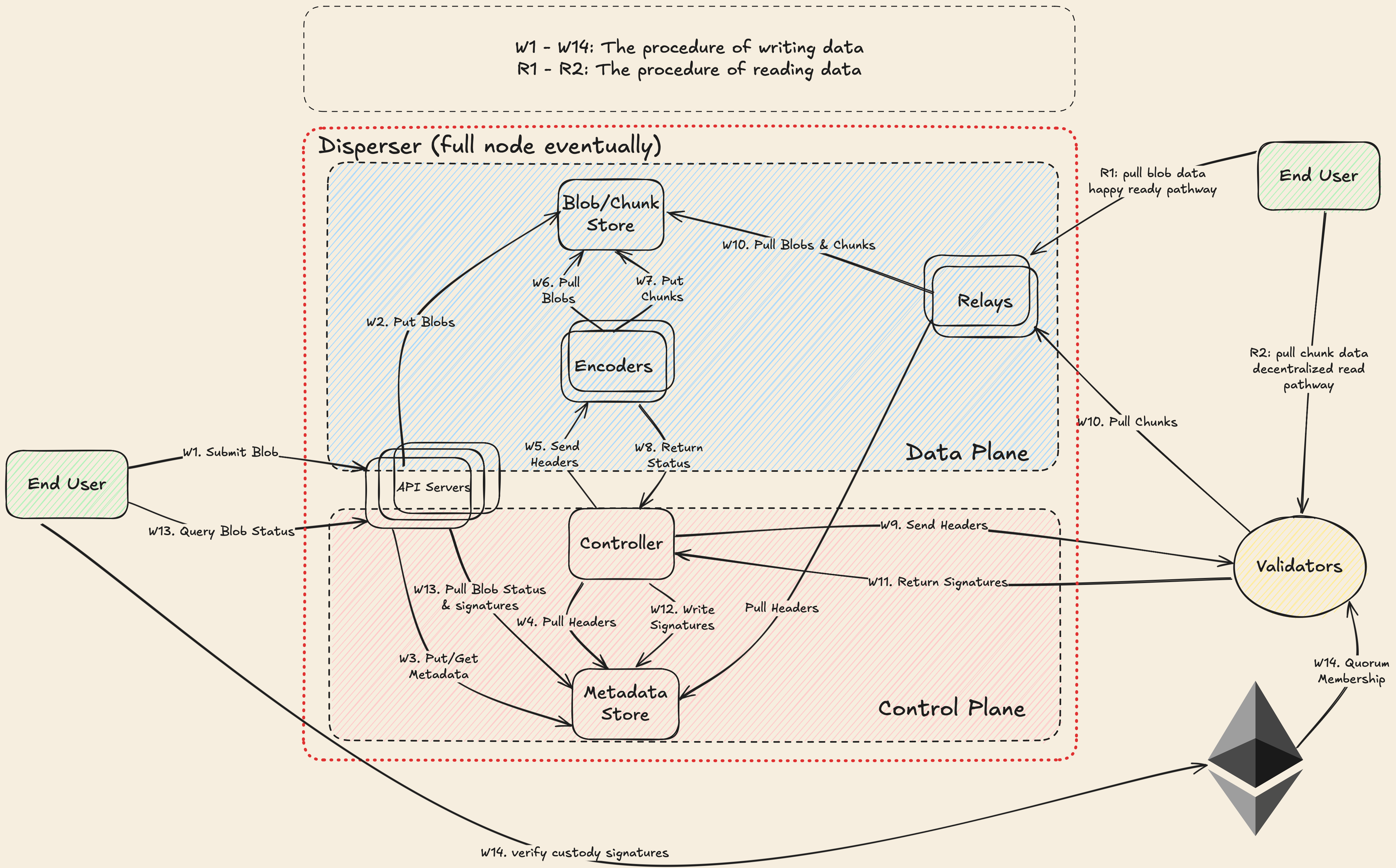
Notes:
- The "end user" for writing and the "end user" for reading can be the same entity. They are shown separately in the diagram for clarity.
- We are planning to build full nodes that will perform the disperser's functionality plus additional duties.
Write
When a user writes data to EigenDA (in the form of a blob), the blob is encoded into chunks and distributed to the validators in accordance with the Chunk Assignment Logic. After enough validators have acknowledged receipt of their chunks and returned their signatures to the disperser, the disperser aggregates the signatures into a data availability (DA) certificate and sends it to the user upon request.
The write process follows the sequence below. The labels in parentheses (e.g., W1, W2) correspond to the steps shown in the diagram above.
-
Disperser Receives Blob (W1, W2, W3). The disperser receives a blob consisting of a
BlobHeaderandBlobData. As a precaution, the disperser can validate thePaymentMetadatacontained in theBlobHeaderto ensure that the blob is properly funded, and that the KZG commitments in theBlobHeaderare correct. Note that validators may still reject payment data as invalid even if approved by the disperser, since the disperser lacks knowledge of global payment state (see Payment System for more details). -
Disperser Encodes Blob (W6, W7). The disperser references the Chunk Assignment Logic to translate the
BlobHeaderinto a set ofEncodingParams. The disperser then encodes the blob according to the Encoding Module and theEncodingParamsto produce a collection of encodedChunks. -
Disperser Serves Chunks. The disperser makes the encoded chunks available via the relay's
GetChunksinterface. This is an authenticated and rate-limited interface where each validator can only request its allocated amount of data. -
Disperser Constructs Blob Certificate. The disperser constructs a
BlobCertificateconsisting of theBlobHeaderand aRelayKey, which can be used to identify the relay URI where the associated chunks are available. -
Disperser Constructs Batch Header. The disperser constructs a
BatchHeaderconsisting of a Merkelized collection ofBlobCertificates and aReferenceBlockNumber, which anchors all blobs in the batch to a specific stake distribution on EigenLayer. -
Disperser Sends Batch Header (W9). The disperser sends the
BatchHeaderto the validators using theStoreChunksAPI. -
Validators Validate Batch Header. The validators validate the
PaymentMetadatafor eachBlobHeadercontained in the batch. If any blob contains improper payment information, the batch is rejected. -
Validators Download and Validate Chunks (W10, W11). For properly authorized batches, validators reference the Chunk Assignment Logic together with the
QuorumNumbersof eachBlobHeaderto determine which chunks they are responsible for hosting. Validators request all associated encoded chunks from theGetChunksinterface of the appropriate relays and validate that eachChunkmatches the corresponding blob's KZG commitment using the included opening proof. Validators also validate that each chunk has the correct length using the Chunk Assignment Logic. If any chunk is unavailable or cannot be validated, the batch is rejected. -
Validators Sign Batch Header (W12). For batches that successfully complete validation, each validator signs the batch header using the BLS identity registered in the
EigenDAServiceManagerand returns the signature to the disperser. -
Disperser Aggregates Signatures. The disperser aggregates the BLS signatures from the validators and returns a
Certificatecontaining theBatchHeader, aggregate signature, and inclusion information used for verifying that a blob is part of the batch.
Read
To read a blob, a client follows the sequence below. The labels in parentheses (e.g., R1, R2) correspond to the steps shown in the diagram above.
-
Read from Relay (R1). The client attempts to retrieve the blob from the
GetBlobinterface of the relay(s) identified in theBlobHeader. This is the primary and most efficient retrieval method, as the relay stores complete blobs. -
Read from Validators (R2). If the blob is not available from the relay(s), the client falls back to retrieving individual chunks directly from the validators and reconstructing the blob. The client reconstructs chunk assignments for all validators assigned to the blob and downloads chunks in a random order until it has collected enough unique chunks to reconstruct the blob. Each chunk is validated using the included KZG proofs before the blob is reconstructed using the erasure coding scheme. This approach distributes load evenly across validators and terminates as soon as the minimum number of unique chunks are verified.
EigenDA Protocol Contracts
This page describes EigenDA contracts that are managed by EigenDA related actors (see the exact roles).
Warning: This page is incomplete and a work in progress as we are undergoing refactors of our contracts as well as some protocol upgrades. The details will change, but the information contained here should at least help to understand the important concepts.
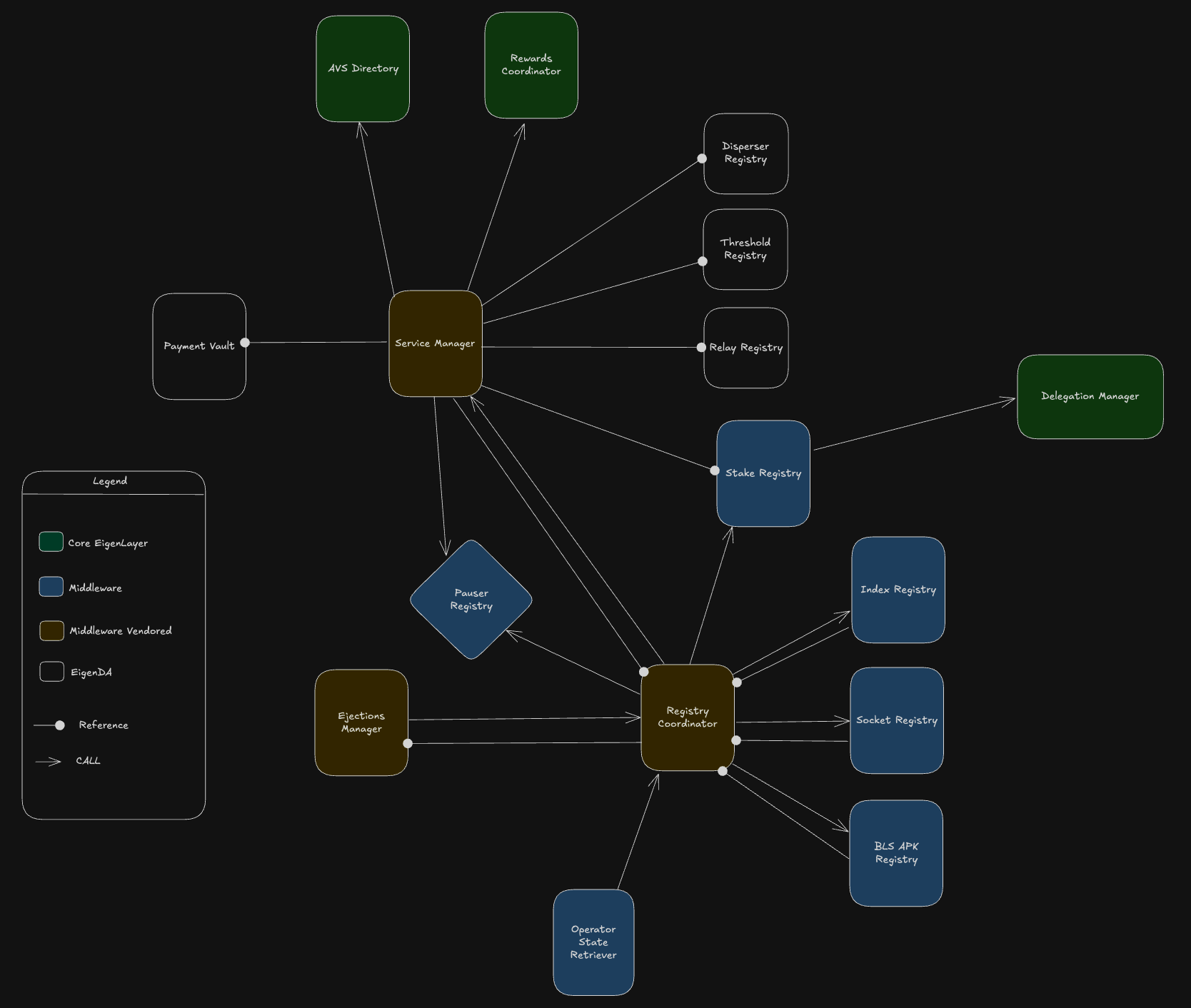
Overview
Middleware Contracts
We make use of eigenlayer-middleware contracts, which are fully documented here and described here. These contracts provide standard interfacing logic for operator state management and AVS representation.
Middleware Vendored Contracts
Some of the middleware contracts (e.g, EjectionsManager, RegistryCoordinator) have been directly vendored into the EigenDA project with minor modifications made.
EigenDA Specific Contracts
The smart contracts can be found in our repo, and the deployment addresses on different chains can be found in the Networks section of our docs.
Integration Contracts
For EigenDA-related contracts that are managed by rollups, see the rollup managed contracts page.
The EigenDA team maintains one customer-facing contract, EigenDACertVerifier. However, using this contract directly is not recommended. The EigenDACertVerifier includes a certVersion parameter that, if upgraded without corresponding updates to a rollup’s offchain code, can lead to liveness outages. Relying on this contract places a rollup’s safety and liveness on EigenDA governance, which is generally discouraged.
Contracts Overview
| Contract Name | Project Category | Deployed Behind ERC1967 Proxy? | Used by Offchain EigenDA Protocol? |
|---|---|---|---|
| EigenDA Directory | eigenda | Yes | Yes |
| Service Manager | eigenda | Yes | Yes |
| Threshold Registry | eigenda | Yes | Yes |
| Relay Registry | eigenda | Yes | Yes |
| Disperser Registry | eigenda | Yes | Yes |
| Payment Vault | eigenda | Yes | Yes |
| Pauser Registry | middleware | No | No |
| BLS APK Registry | middleware | Yes | Yes |
| Index Registry | middleware | Yes | Yes |
| Stake Registry | middleware | Yes | Yes |
| Socket Registry | middleware | Yes | Yes |
| Operator State Retriever | middleware | No | Yes |
| Registry Coordinator | vendored middleware | Yes | Yes |
| Ejections Manager | vendored middleware | Yes | No |
| Cert Verifier Router | integrations | Yes | No |
EigenDADirectory
Description
This contract serves as the central discovery and reference point for all contracts composing the EigenDA system. It implements a lightweight namespace resolution protocol in which human-readable string keys are mapped to EigenDA contract addresses.
Access Mgmt
Ownablerole that can do unilateral entry key modifications
Offchain Usage
This dynamic naming pattern requires off-chain management of canonical contract keys, allowing clients and services to retrieve on-chain system context from a single directory contract reference rather than requiring every contract address to be hard-coded or passed through environment configuration.
EigenDAServiceManager
Description Used for onchain AVS registration with the EigenLayer protocol, EigenDA V1 batching, storing protocol params, rewards distribution, and referencing EigenDA protocol contracts:
- Inherits the
ServiceManagerBasefor operator registration and rewards distribution. - Manages batch settlement roles with callable function (i.e,
confirmBatch) that allows for EigenDA V1 batches to be confirmed and settled into a storage commitment sequence. - Stores protocol params (i.e,
BLOCK_STALE_MEASURE,BLOCK_STORE_DURATION) for offchain ingestion by DA validator nodes. - Stores non-callable references to other EigenDA protocol contracts in storage (i.e,
DisperserRegistry,ThresholdRegistry,RelayRegistry,StakeRegistry,PaymentVault).
Access Mgmt
Pauserrole that can halt EigenDA V1 batch settlementOwnablerole that can modify batch confirmer EOA allow-list, AVS metadata,RewardsClaimee, andRewardsInitiatorRegistryCoordinatorrole that can register/de-register operators through routed calls to theAVSDirectory(i.e,RegistryCoordinator->EigenDAServiceManager->AVSDirectory)RewardsInitiatorrole that can create operator directed and general AVS rewards via routed calls to theRewardsCoordinatorcontract (i.e,RewardsInitiator->EigenDAServiceManager->RewardsCoordinator)
Offchain Usage
TODO
EigenDAThresholdRegistry
Description
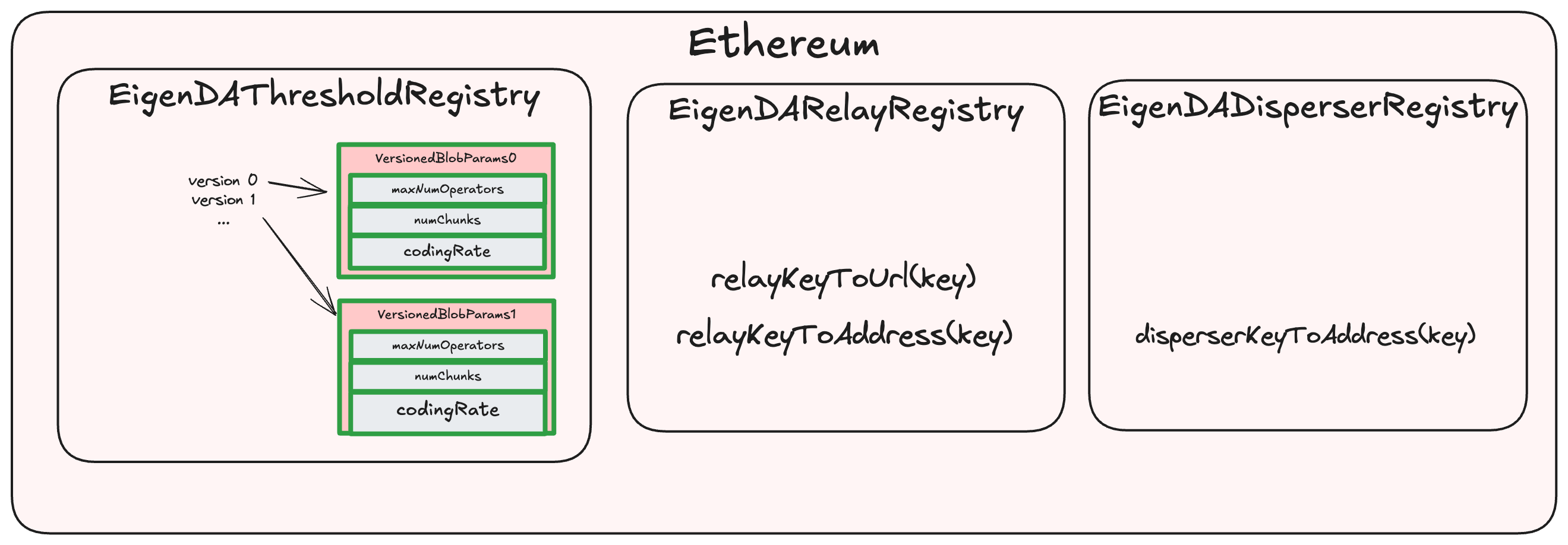
The EigenDAThresholdRegistry contains two sets of protocol parameters:
/// @notice mapping of blob version id to the params of the blob version
mapping(uint16 => VersionedBlobParams) public versionedBlobParams;
struct VersionedBlobParams {
uint32 maxNumOperators;
uint32 numChunks;
uint8 codingRate;
}
/// @notice Immutable security thresholds for quorums
SecurityThresholds public defaultSecurityThresholdsV2;
struct SecurityThresholds {
uint8 confirmationThreshold;
uint8 adversaryThreshold;
}
The securityThresholds are currently immutable. Confirmation and adversary thresholds are sometimes also referred to as liveness and safety thresholds:
- Confirmation Threshold (aka liveness threshold): minimum percentage of stake which an attacker must control in order to mount a liveness attack on the system.
- Adversary Threshold (aka safety threshold): total percentage of stake which an attacker must control in order to mount a first-order safety attack on the system.
Their default values are currently set as:
defaultSecurityThresholdsV2 = {
confirmationThreshold = 55,
adversaryThreshold = 33,
}
A new BlobParam version is rarely introduced by the EigenDA Foundation Governance. When dispersing a blob, rollups explicitly specify the version they wish to use. Currently, only version 0 is defined, with the following parameters (reference):
versionedBlobParams[0] = {
maxNumOperators = 3537,
numChunks = 8192,
codingRate = 8,
}
The five parameters are intricately related by this formula which is also verified onchain by the verifyBlobSecurityParams function:
where
EigenDARelayRegistry
Description
Contains EigenDA network registered Relays' Ethereum address and DNS hostname or IP address. BlobCertificates contain relayKeys, which can be transformed into that relay's URL by calling relayKeyToUrl.
Access Mgmt
Ownablerole that can register new relay entries
Offchain Usage
TODO
EigenDADisperserRegistry
Description
Contains EigenDA network registered Dispersers' Ethereum address. The EigenDA Network currently only supports a single Disperser, hosted by EigenLabs. The Disperser's URL is currently static and unchanging, and can be found on our docs site in the Networks section.
Access Mgmt
Ownablerole that can register new dispersers
Offchain Usage
TODO
PaymentVault
Description
Payment contract used to escrow on-demand funds, hold user reservations, and define global payment parameters used by the network (i.e, globalSymbolsPerPeriod, reservationPeriodInterval, globalRatePeriodInterval).
Access Mgmt
Ownablerole that can set payment reservations
Offchain Usage
TODO
PauserRegistry
Description Manages a stateful mapping of pausers that can be arbitrarily added or revoked. This contract is assumed to be deployed immutably. The pauser mapping is checked by caller:
- Mapping checked as prerequisite for pausing batch confirmation logic in
EigenDAServiceManager - Mapping checked as prerequisite for pausing operator state update logic in
RegistryCoordinator
Access Mgmt
Unpauser(or admin) role that can set / remove existing pausers
Offchain Usage
TODO
BLSApkRegistry
Description
This contract stores each operator's BLS public key as well as per quorum aggregate public keys which are only updatable by the RegistryCoordinator.
Access Mgmt
RegistryCoordinatorrole that can invoke aggregate key updates via the registration/de-registration of operators
Offchain Usage
TODO
IndexRegistry
Description Maintains an ordered, historically versioned list of operators for each quorum, allowing the RegistryCoordinator to register or deregister operators while preserving full block-by-block history of operator counts and index assignments. It provides efficient read functions to reconstruct the operator set at any block.
Access Mgmt
RegistryCoordinatorrole that makes stateful updates when registering / deregistering quorum operators
Offchain Usage
TODO
StakeRegistry
Description Stores stake updates bounded by block number and quorum strategy:
struct StakeUpdate {
// the block number at which the stake amounts were updated and stored
uint32 updateBlockNumber;
// the block number at which the *next update* occurred.
/// @notice This entry has the value **0** until another update takes place.
uint32 nextUpdateBlockNumber;
// stake weight for the quorum
uint96 stake;
}
Access Mgmt
Ownablerole that can deploy and modify staking strategiesRegistryCoordinatorrole that makes stateful updates when registering / deregistering quorum operators
Offchain Usage
TODO
SocketRegistry
Description
Stores stateful mapping of operator ID => socket where socket is the operator's DNS hostname.
Access Mgmt
RegistryCoordinatorrole that makes stateful updates when registering / deregistering quorum operators
Offchain Usage
TODO
OperatorStateRetriever
Description
A stateless read-only contract that does exhaustive lookups against the registry coordinator for fetching operator metadata. This bundles stored procedure logic to avoid exhaustive RPC calls made to view functions by offchain EigenDA services.
Access Mgmt
N/A
Offchain Usage
TODO
EigenDARegistryCoordinator
Description
This contract orchestrates operator lifecycle across EigenDA's stake, BLS key, index, and socket registries - handling:
- registration, deregistration
- churning
- stake-updates
- quorum creation/config
- historical quorum-bitmap tracking
Access Mgmt
Pauserrole that can halt operator state updatesOwnablerole that can add new quorums, operator set params, & ejector params / role changesEjectorrole that can invoke an ejection function to forcibly deregister an operator
Offchain Usage
TODO
EigenDAEjectionsManager
Description
Coordinates the lifecycle of ejecting non-responsive operators from EigenDA. It allows an Ejector role to queue and complete ejections. Each queued ejection has a corresponding bond attached by the Ejector where a targeted operator can cancel the ejection by providing a signature before it becomes "confirmable" after a number of DelayBlocks.
Access Mgmt
Ownablerole that can change public parameters (i.e,DelayBlocks,CooldownBlocks)Ejectorrole that can invoke an ejection function to forcibly deregister an operator
Offchain Usage
TODO
CertVerifierRouter
Description
See here.
Access Mgmt
Ownablerole that can add newEigenDACertVerifierentries at new activation block number
Offchain Usage
This dynamic naming pattern requires off-chain management of canonical contract keys, allowing clients and services to retrieve on-chain system context from a single directory contract reference rather than requiring every contract address to be hard-coded or passed through environment configuration.
Governance Roles
There are four key governance roles in the EigenDA contracts seen across network environments (i.e, mainnet, hoodi-testnet, hoodi-preprod, sepolia-testnet):
- ERC1967
ProxyAdminthat can upgrade implementation contracts Ownerthat can perform sensitive stateful operations across protocol contractsPauserthat can halt stateful updates on theServiceManagerandRegistryCoordinatorcontracts. This role is managed by the immutablePauserRegistrycontractEjectorthat can initialize and complete ejection requests via theEjectionsManagercontract
Decentralized Validator Set Governance
Overview
EigenDA's validator set governance manages validator entry and exit in a decentralized way. This document describes the ejection and churning protocols that govern how validators leave and join the EigenDA validator set.
The protocol includes:
- Ejection: dispersers may eject under-performing validators, with validators able to cancel ejections.
- Churner: an on-chain function that removes the validator with the smallest amount of stake to allow a validator to join when the validator set is full.
1. Ejection Protocol
The ejection protocol maintains EigenDA's liveness and quality of service by allowing dispersers to eject honest but under-performing validators.
1.1 Protocol Actors
| Actor | Role | Implementation |
|---|---|---|
| Ejector (Disperser) | Monitors validator performance and initiates ejections | ejector/ |
| Ejectee (Validator) | Monitors ejection attempts and defends against unjust ejections | node/ejection/ejection_sentinel.go |
| Ejection Manager | Smart contract coordinating ejection lifecycle | EigenDAEjectionManager.sol |
1.2 Ejection Initiation
The ejection lifecycle is managed by the BeginEjection() method in ejector/ejection_manager.go:127-193, which performs all pre-flight checks before initiating an on-chain ejection.
1.2.1 Ejector Authorization
Only authorized dispersers can initiate ejections. Authorized disperser addresses are stored in an allow-list within the EigenDAEjectionManager contract. Initially, this list contains only the EigenDA disperser operated by EigenLabs. The list can be expanded as additional dispersers become available.
Implementation: The contract enforces this via the onlyEjector modifier (EigenDAEjectionManager.sol:66-69), which checks the EJECTOR_ROLE using AccessControl.
1.2.2 Automatic Ejection Decision-Making
The disperser monitors validator performance over a configurable time window (performance_evaluation_window, default: 10 minutes) and computes each validator's signing_rate.
A validator becomes eligible for ejection only when all of the following conditions are met:
- Zero signing rate: The validator's
signing_rateis zero over the evaluation window - Cool-down period elapsed:
DISPERSER_COOL_DOWNhas passed since the last ejection attempt against this validator - Selective non-participation: Other validators show non-zero signing rates during the same period
These rules prevent ejections during network-wide outages and limit wasted transaction fees when dealing with potentially malicious validators who repeatedly cancel ejections while being under-performing.
Implementation: The evaluation logic is in ejector/ejector.go:102-184. The ejection criterion is implemented as:
// ejector/ejector.go:146
isEjectable := signingRate.GetSignedBatches() == 0 && signingRate.GetUnsignedBatches() > 0
This ensures a validator is only ejectable if they signed zero batches but there were batches to sign (selective non-participation). The evaluation window is configured via EjectionCriteriaTimeWindow in ejector/ejector_config.go:41-45.
1.2.3 Non-Ejection List
The disperser maintains a non-ejection list to handle validators that repeatedly cancel ejections without actually performing their duties. When a validator's failed ejection attempts reach MAX_FAILURE_TIMES, they are added to this list and automatic ejection stops. Human intervention is then required to deal with these validators. This list can also be manually configured.
Implementation: The non-ejection list (called ejectionBlacklist) is maintained in ejector/ejection_manager.go:54-60. Failed attempts are tracked in the failedEjectionAttempts map (lines 68-72), and validators are added to the blacklist in handleAbortedEjection (lines 384-412). The threshold is configured via MaxConsecutiveFailedEjectionAttempts in ejector/ejector_config.go:53-54, with a default value of 5.
1.2.4 Manual Ejection
In addition to automatic ejection based on performance monitoring, dispersers can manually initiate ejections against specific validators.
1.3 Ejection Logic in the Smart Contract
The EigenDAEjectionManager contract enforces the following constraints before accepting an ejection request:
- Rate Limiting: At least
EJECTION_COOL_DOWN(30 minutes) must have passed since the previous ejection attempt against the same validator - Concurrency Control: At most one active ejection is allowed per validator at any given time
Upon accepting a valid ejection request, the contract:
- Records the ejection in contract storage
- Starts a cancellation window of duration
RESPONSE_TIME(30 minutes) - Emits an ejection event that validators monitor
Implementation: The constraint checks are enforced in EigenDAEjectionLib.sol:
// EigenDAEjectionLib.sol:36-42
require(ejectee.record.proceedingTime == 0, "Ejection already in progress");
require(ejectee.lastProceedingInitiated + s().cooldown <= block.timestamp, "Ejection cooldown not met");
ejectee.record.ejector = ejector;
ejectee.record.quorums = quorums;
ejectee.record.proceedingTime = uint64(block.timestamp) + s().delay;
ejectee.lastProceedingInitiated = uint64(block.timestamp);
The first require enforces concurrency control (one ejection per validator), the second enforces the cooldown period, and the delay parameter sets the cancellation window duration.
1.4 Validator Defense (Cancellation)
1.4.1 Ejection Monitoring
Each validator node runs an ejection sentinel (node/ejection/ejection_sentinel.go) that continuously monitors the EigenDAEjectionManager contract for ejection events targeting that validator.
1.4.2 Cancellation Modes
Validators operate in one of two modes, configurable via a trusted dispersers list:
| Mode | Condition | Behavior |
|---|---|---|
| Mode 1 | Ejector is in trusted dispersers list | No cancellation sent (validator trusts ejector's judgment) |
| Mode 2 | Ejector is not in trusted dispersers list | Cancel if validator is online and running compliant software version |
Default Configuration: The trusted dispersers list is empty by default, meaning validators operate in Mode 2 for all ejectors.
Note: Validators must configure a wallet to submit cancellation transactions. Until most validators have set up their cancellation infrastructure, only the EigenDA disperser will be authorized as a valid ejector.
1.4.3 Cancellation Process
To cancel an ejection, the validator:
-
Generates cancellation message containing:
- Chain ID (identifying which L1 blockchain)
- Validator's address
- Block height at which the ejection was initiated
-
Signs the message using the validator's BLS private key
-
Submits transaction to
EigenDAEjectionManagercontaining the signed cancellation message
If the cancellation is received within the RESPONSE_TIME window and the signature is valid, the ejection is canceled and the validator remains in the validator set.
1.5 Ejection Finalization
If no valid cancellation is received before the RESPONSE_TIME window expires, any disperser can finalize the ejection by submitting a finalizing transaction to the contract. Upon finalization, the validator is deregistered from the EigenDA validator set via a call to EigenDARegistryCoordinator.
1.6 Rejoining After Ejection
Validators that have been ejected are subject to a cool-down period of 1 day before they can rejoin the validator set.
1.7 Protocol Parameters
| Parameter | Value | Description | Implementation |
|---|---|---|---|
RESPONSE_TIME | 30 minutes | Cancellation window duration | delay in EigenDAEjectionStorage.sol:40-42 |
EJECTION_COOL_DOWN | 30 minutes | Minimum time between ejection attempts for same validator | cooldown in EigenDAEjectionStorage.sol:40-42 |
DISPERSER_COOL_DOWN | 24 hours (default) | Cool-down before retrying ejection after failed attempt | EjectionRetryDelay in ejector/ejector_config.go:50-51 |
MAX_FAILURE_TIMES | 5 (default) | Failed ejection attempts before adding to non-ejection list | MaxConsecutiveFailedEjectionAttempts in ejector/ejector_config.go:53-54 |
performance_evaluation_window | 10 minutes (default) | Time window for computing signing rate | EjectionCriteriaTimeWindow in ejector/ejector_config.go:41-45 |
| Rejoin cool-down | 1 day | Wait time before ejected validator can rejoin | (Contract-level parameter) |
1.9 Implementation References
| Component | Path |
|---|---|
| Ejector service | ejector/ |
| Ejection sentinel | node/ejection/ejection_sentinel.go |
| Ejection manager contract | contracts/src/periphery/ejection/EigenDAEjectionManager.sol |
| Ejection library | contracts/src/periphery/ejection/libraries/EigenDAEjectionLib.sol |
| Ejection types | contracts/src/periphery/ejection/libraries/EigenDAEjectionTypes.sol |
| Ejection storage | contracts/src/periphery/ejection/libraries/EigenDAEjectionStorage.sol |
2. Churning Protocol
The churning protocol governs how new validators join the EigenDA validator set when the maximum validator capacity has been reached. The churning logic is computed entirely on-chain.
2.1 Overview
When the validator set is at maximum capacity, a new validator can only join by "churning out" an existing validator with the smallest stake. The smart contract automatically identifies and ejects the smallest-stake validator to make room for the higher-stake incoming validator.
2.2 On-Chain Churn Selection
The EigenDARegistryCoordinator contract implements the churn selection logic:
- A new validator attempts to register and the validator set is at capacity
- The contract iterates through all current validators in the set and identifies the validator with the smallest stake
- Automatically deregisters the smallest-stake validator
- Registers the new validator
Implementation: The main registration logic is in registerOperator() (EigenDARegistryCoordinator.sol:108-142), which checks if the operator count exceeds maxOperatorCount and calls _churnOperator(). The _churnOperator() function performs an exhaustive search:
// EigenDARegistryCoordinator.sol:157-178
function _churnOperator(uint8 quorumNumber) internal {
bytes32[] memory operatorList = indexRegistry().getOperatorListAtBlockNumber(quorumNumber, uint32(block.number));
require(operatorList.length > 0, "RegCoord._churnOperator: no operators to churn");
// Find the operator with the lowest stake
bytes32 operatorToChurn;
uint96 lowestStake = type(uint96).max;
for (uint256 i; i < operatorList.length; i++) {
uint96 operatorStake = stakeRegistry().getCurrentStake(operatorList[i], quorumNumber);
if (operatorStake < lowestStake) {
lowestStake = operatorStake;
operatorToChurn = operatorList[i];
}
}
// Deregister the operator with the lowest stake
bytes memory quorumNumbers = new bytes(1);
quorumNumbers[0] = bytes1(uint8(quorumNumber));
_deregisterOperator({operator: blsApkRegistry().pubkeyHashToOperator(operatorToChurn), quorumNumbers: quorumNumbers});
}
This iterates through all operators to find the one with minimum stake and automatically deregisters them.
EigenDA Payment System
1. Overview
The EigenDA payment system allows users to pay for blob dispersals through two methods: reservations and on-demand
payments. All payment logic is implemented in the core/payments package.
Key Concepts:
- Blob sizes are measured in symbols, where each symbol is 32 bytes.
- Blob sizes are measured post-blob encoding.
- Blob sizes are constrained to powers-of-two: dispersals are rounded up to the next power-of-two number of symbols when computing size.
- The PaymentVault contract
stores all on-chain payment-related data:
- User reservation parameters
- User on-demand deposits
- Global payment parameters, including but not limited to:
minNumSymbols: dispersals smaller than this threshold are billed as if they wereminNumSymbolsin sizepricePerSymbol: the price per symbol (in wei) for on-demand payments
2. Payment Methods
2.1 Reservation Payments
- Reservations provide guaranteed bandwidth for a specified time period.
- Users reserve capacity in advance, and must "use it or lose it".
- Reservations are procured out-of-band, through Eigen Labs.
- The system uses a leaky bucket algorithm to manage usage:
symbols are added to the bucket each time a blob is dispersed, and these leak out over time. A user can only make a
dispersal if the leaky bucket has available capacity.
- The total capacity of the leaky bucket is parameterized by reservation rate and duration. The size of the
bucket in symbols is
reservationRate * bucketDuration. This calculation controls the burstiness of reservation usage.
- The total capacity of the leaky bucket is parameterized by reservation rate and duration. The size of the
bucket in symbols is
- Parameters describing active user reservations are kept in the
PaymentVaultcontractsymbolsPerSecond: the reservation bandwidth ratestartTimestampandendTimestamp: define when the reservation is activequorumNumbers: which quorums the reservation can be used for
2.1.1 Source of Truth
- Validator nodes are the source of truth for reservation usage.
- Each validator keeps track of the dispersals from each user account, and will reject dispersals if the user doesn't have enough capacity.
- Clients keep a local reckoning of their own reservation usage, so that they can stay within the bounds of their reserved bandwidth.
- Dispersers also keep a local reckoning of client reservation usage, but a malicious client can bypass this check by intentionally dispersing too much data spread out over multiple dispersers. From the perspective of any given disperser, the client is within reservation limits. But in total, the client is over the limit. This isn't a problem, because validator nodes will catch the misbehavior. By having dispersers keep track of reservation usage, we are imposing a limit on how severely a client can misbehave in this way: in a system with N dispersers, a malicious client can disperse at most N * reservation rate.
- Reservation usage state agreement: since clients keep a local reckoning of reservation usage without any input from
validators, it's all but guaranteed that their local state will differ (at least slightly) from the state on any given
validator. This actually doesn't present a problem, so long as these key invariants are maintained:
- A client behaving honestly must be able to disperse blobs without payment failures.
- The amount of "free" dispersals that can be stolen by a dishonest client must be tightly limited.
2.1.2 Bucket Capacity Configuration
- We can achieve these invariants by using buckets of differing sizes between clients and validator nodes. If we make validator buckets larger than client buckets by some multiple, then slight discrepancies between client and validator are naturally smoothed out.
- If a dishonest client tries to disperse more data than allowed, the behavior will be permitted by validators for a short time, but eventually even the larger validator bucket will fill. At that point, validators will limit new dispersals from the dishonest client to the rate of the reservation, and no additional dispersals may be stolen.
- The capacity difference between client and validator buckets must be chosen to accommodate the maximum
expected latency of the system. Specifically:
validatorBucketCapacity - clientBucketCapacity = reservationRate * maxSystemLatency - This ensures that honest clients operating at full capacity won't be rejected due to timing discrepancies.
- Current bucket size configuration:
- Client buckets use a duration of 1 minute.
- Disperser buckets use a duration of 1.5 minutes.
- Validator buckets use a duration of 2 minutes, accommodating up to 1 minute of system latency.
2.1.3 Leaky Bucket Overfill
The reservation leaky bucket implementation permits clients to overfill their buckets, with certain constraints:
- If a client has any available capacity in their bucket, they may make a single dispersal up to the maximum blob size, even if that dispersal causes the bucket to exceed its maximum capacity.
- When this happens, the bucket level actually goes above the maximum capacity, and the client must wait for the bucket to leak back down below full capacity before making the next dispersal.
- This feature exists to solve a problem with small reservations: without overfill, a reservation might be so small that its total bucket capacity is less than the max blob size, which would prevent the user from dispersing blobs up to max size.
- By permitting a single overfill, even the smallest reservation can disperse blobs of maximum size.
2.1.4 Reservation Usage Persistence
The leaky bucket algorithm does not require persisting reservation usage state across system restarts. Different system components initialize their buckets with opposing biases to maintain system integrity without persistence:
Client Initialization (Conservative Bias)
- Clients initialize their leaky bucket as completely full (no capacity available) upon restart.
- They must wait for symbols to leak out before dispersing, guaranteeing compliance with reservation rate limits.
- While this may result in slight underutilization if usage was low before restart, it prevents violation of reservation limits.
Validator Initialization (Permissive Bias)
- Validators initialize leaky buckets as completely empty (full capacity available) upon restart.
- This ensures they never incorrectly deny service to users entitled to a reservation.
- In the worst case, a malicious client timing dispersals with validator restarts might be able to cause a small amount of extra work for that specific validator.
This dual-bias approach eliminates the complexity of distributed reservation state persistence.
2.2 On-Demand Payments
- On-demand payments allow users to pay per dispersal from funds deposited in the PaymentVault contract.
- Once deposited, funds cannot be withdrawn - they can only be used for dispersals or abandoned.
- Limited to quorums 0 (ETH) and 1 (EIGEN)
- Custom quorums are not supported for on-demand payments because quorum resources are closely tailored to expected usage. Allowing on-demand payments could enable third parties to overutilize these limited resources.
- Costs are calculated based on blob size (in symbols) multiplied by the
pricePerSymbolparameter in PaymentVault. - Payment usage is not tracked on-chain; instead, the EigenDA Disperser maintains a DynamoDB table recording total historical usage for all clients.
- When processing a dispersal, the Disperser compares a user's total historical usage against their on-chain deposits in the PaymentVault to determine if they have sufficient funds.
- Clients fetch the latest cumulative payment state from the EigenDA Disperser on startup via the
GetPaymentStateRPC.
2.2.1 Why Only the EigenDA Disperser?
- On-demand payments are supported only through the EigenDA Disperser.
- Since EigenDA currently lacks a consensus mechanism, validators cannot easily coordinate to limit total on-demand throughput across the network.
- Therefore, the EigenDA Disperser fills the role of arbiter, ensuring that total network throughput doesn't exceed configured levels.
2.2.2 Cumulative Payment
The cumulative payment is a field set in the PaymentHeader by the client when making a dispersal. It represents the total cost (in wei) of all previous dispersals, plus the new dispersal.
- Historical context: In a prior payments implementation, the cumulative payment field included by the client in the PaymentHeader had to be monotonically increasing, and the disperser would verify that each new cumulative payment received exceeded the previous one by at least the cost of the new blob. This severely limited concurrency, since clients had to make sure that all on-demand dispersals were handled by the disperser in strict order. In practice, that meant waiting for the entire network roundtrip, for dispersal N to be confirmed before submitting dispersal N+1.
- Current implementation: The system has been simplified to improve concurrency:
- Clients still populate the
cumulative_paymentfield with their local calculation of cumulative payment. - However, the Disperser now only checks if this field is non-zero (to determine payment type) and ignores the exact value.
- The Disperser tracks each account's on-demand usage in DynamoDB, incrementing by the blob cost for each dispersal.
- This removes the strict ordering requirement and allows for highly concurrent dispersals.
- Clients still populate the
- Why clients still populate the field: Although currently unused beyond the zero/non-zero check, clients continue to populate this field with meaningful values. This preserves the option to reintroduce cumulative payment validation in the future if needed.
3. Client Payment Strategy
3.1 Payment Header
Each dispersal request includes a PaymentHeader containing:
account_id: Ethereum address identifying the payment accounttimestamp: Nanosecond UNIX timestamp (serves as nonce)cumulative_payment: Variable-length big-endian uint for on-demand dispersal (or empty for reservation dispersal)
The payment header implicitly specifies which payment mechanism is being used:
- If
cumulative_paymentis empty/zero → reservation payment - If
cumulative_paymentis non-zero → on-demand payment
3.2 Client Configuration Options
Clients can configure their payment strategy in three ways:
-
Reservation-only: Client exclusively uses reservation payments.
cumulative_paymentfield is always left empty.- Dispersals fail if reservation capacity is exhausted.
-
On-demand-only: Client exclusively uses on-demand payments.
cumulative_paymentfield is always populated.- All dispersals charged against deposited balance.
-
Hybrid with fallback: Client uses both payment methods.
- Primary: Uses reservation while capacity is available.
- Fallback: Automatically switches to on-demand when reservation is exhausted.
- Ensures continuous operation without manual intervention.
EigenDA Payment System Migration
1. Overview
EigenDA is migrating from a fixed bin reservation accounting model to a leaky bucket algorithm. The new payment system is being implemented to be compatible with permissionless dispersal. While making changes to support this new feature, the opportunity to reduce accumulated tech debt is being seized.
Key Changes:
- Reservation accounting switches from fixed time bins to continuous leaky bucket rate limiting
- Validators become the source of truth for reservation metering (previously the EigenDA Disperser)
- On-demand payment logic remains unchanged
- Payment logic is being reorganized or reimplemented, to reduce tech debt
2. Legacy Payment System
The legacy implementation uses a fixed bin model where:
- Users disperse against reservation bandwidth allotted for the current fixed time bin
- Once capacity for the current bin is exhausted, users must wait for the next bin to arrive, to disperse more data
- Implementation split between
core/meterer/andapi/clients/v2/accountant.go
Weaknesses:
- Bursty behavior at bin boundaries creates uneven load distribution
- Network-wide bin synchronization causes simultaneous bursts across all users, exacerbating the problem of bursts
3. New Payment System
The new payment system is implemented in the core/payments/ package.
Within this new implementation, reservation payments are managed with a leaky bucket algorithm, instead of using fixed bins. This alternate algorithm smooths out bursts with smooth capacity recovery:
- Bursts are less severe bursts for each individual user: the maximum burst size from a single user is now limited by the size of the leaky bucket, compared to the fixed bin algorithm where maximum burst is 2x bin size
- Network wide bursts are unlikely to be simultaneous, since there aren't synced bin boundaries
4. Migration Considerations
Requirements
- Backward compatibility: Old clients will work seamlessly with new disperser logic
- Users operating well below reservation limits will experience no interruption, and may choose to update clients whenever convenient
- Users operating near reservation limits may experience some degraded behavior, if the local algorithm disagrees with the updated remote algorithm. Such users may resolve degraded behavior by updating client code to match the new algorithm.
- Gradual rollout: Phased deployment with feature flags for safety
5. Migration Rollout Process
Phase 1: Client & Disperser Release
- Client release with leaky bucket accounting
- Disperser release with leaky bucket support
Phase 2: Validator Release
- Deploy after client/disperser adoption complete
- Feature flag controls activation
- Once this phase is complete, validators have become authoritative source for reservation metering
- This must occur before a second Disperser is brought online
EigenDA V1
The EigenDA V1 system is deprecated and in the process of being completely sunset. We recommend all users migrate to EigenDA Blazar ("V2"), which is what is described in this book.
For completion, and for those interested in comparing the V1 and V2 systems, we leave the V1 architecture diagram below.
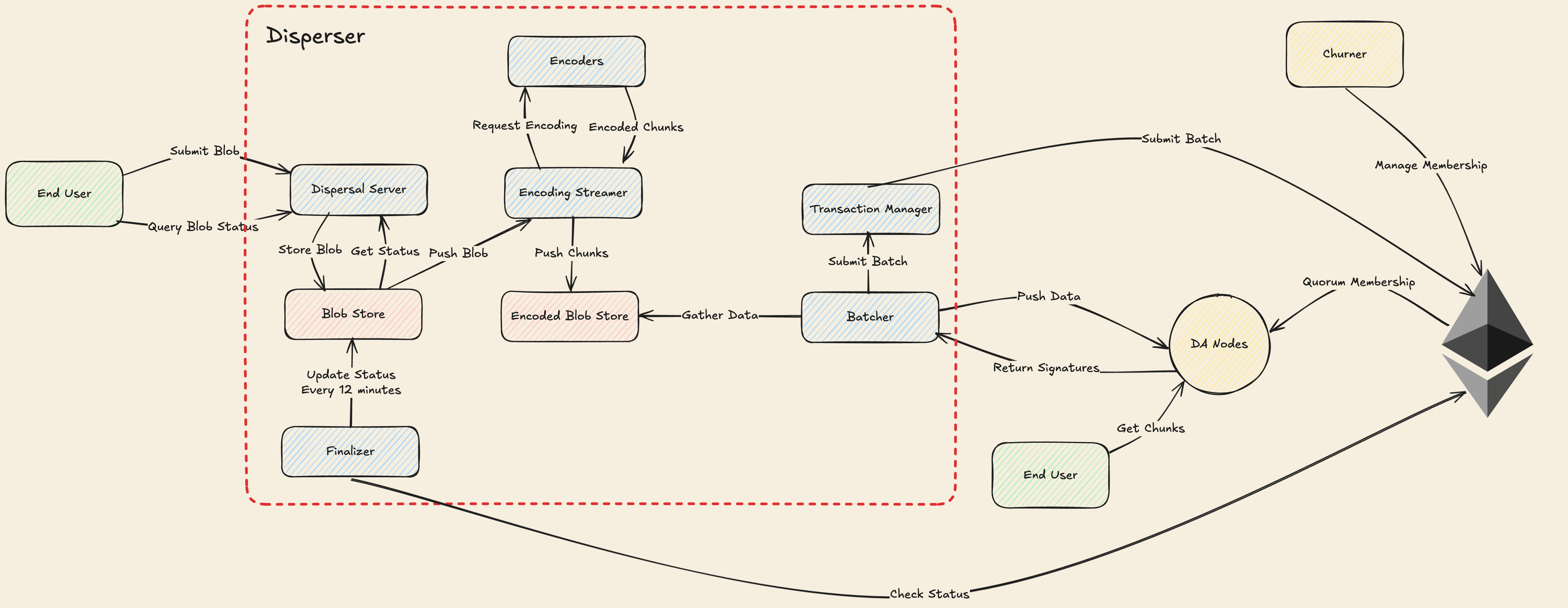
EigenDA Integrations
This section is meant to be read by eigenda and rollup developers who are writing or extending an integration with EigenDA. Users and developers who just want to understand how an integration works at a high level, and need to learn how to configure their own integration, should instead visit our Integrations Guides.
EigenDA V2 Integration Spec
Overview
The EigenDA V2 release documentation describes the architectural changes that allow for important network performance increases. From the point of view of rollup integrations, there are three important new features:
- Blob batches are no longer bridged to Ethereum with dispersals now being confirmed once a batch has been
CERTIFIED(i.e, signed over by operator set). This operation takes 10-20 seconds - providing lower confirmation latency and higher throughput for the rollup. Verification of the blobs now needs to be done by the rollup stack. - Centralized (accounting done by disperser) payments model
- A new relay API from which to retrieve blobs (distinct from the disperser API which is now only used to disperse blobs)
Diagrams
We will refer to the below diagrams throughout the spec.
High Level Diagram
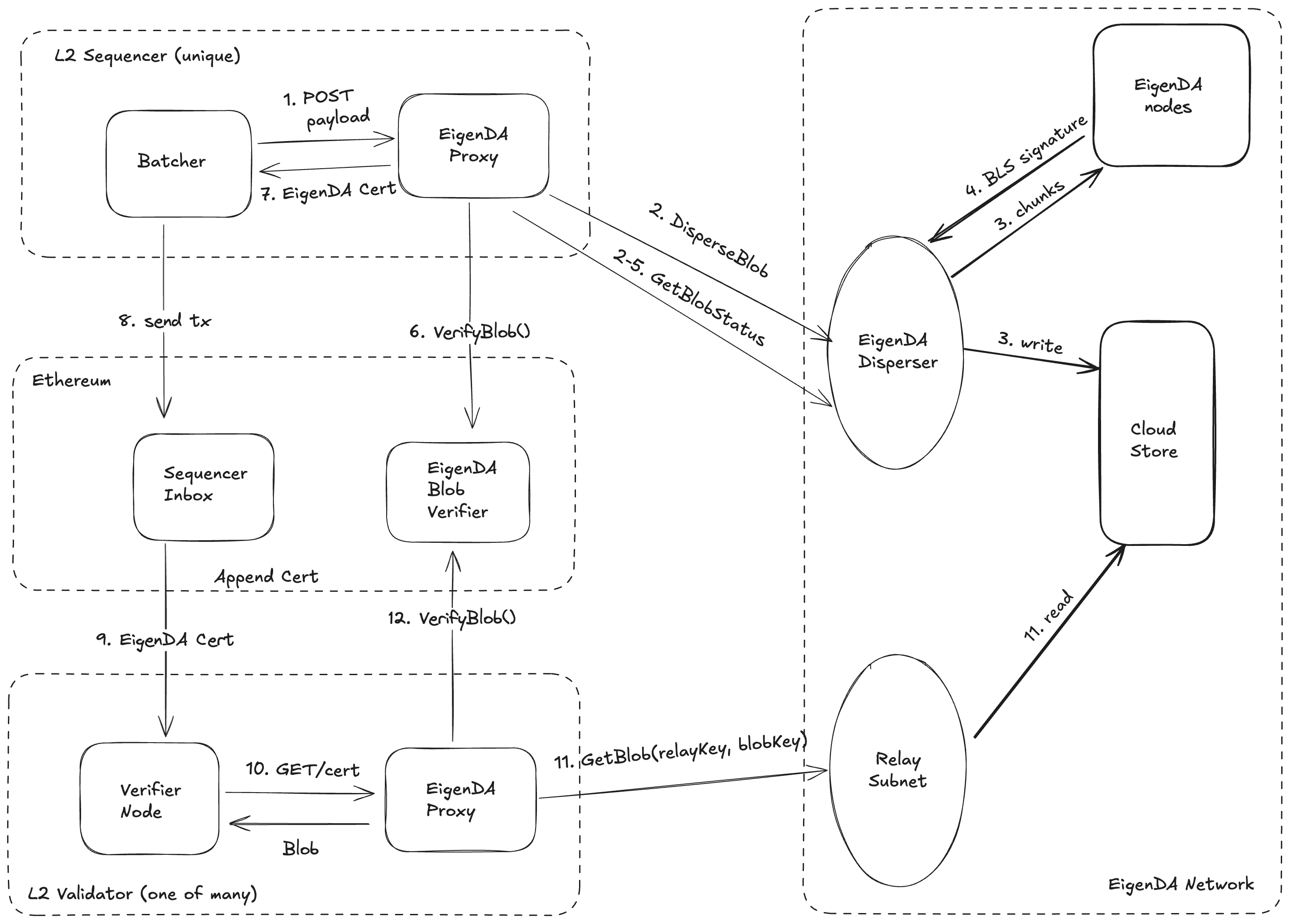
Sequence Diagram
sequenceDiagram
box Rollup Sequencer
participant B as Batcher
participant SP as Proxy
end
box EigenDA Network
participant D as Disperser
participant R as Relay
participant DA as DA Nodes
end
box Ethereum
participant BI as Batcher Inbox
participant BV as EigenDABlobVerifier
end
box Rollup Validator
participant VP as Proxy
participant V as Validator
end
%% Blob Creation and Dispersal Flow
B->>SP: Send payload
Note over SP: Encode payload into blob
Note over SP: Compute commitment locally using SRS points
Note over SP: Create blob_header including payment_header
SP->>D: DisperseBlob(blob, blob_header)
D-->>SP: QUEUED status + blob_header_hash
%% Parallel dispersal to Relay and DA nodes
par Dispersal to Storage
R->>D: Pull blob
and Dispersal to DA nodes
D->>DA: Send Headers
DA->>R: Pull Chunks
DA->>D: Signature
end
loop Until CERTIFIED status
SP->>D: GetBlobStatus
D-->>SP: status + signed_batch + blob_verification_info
end
SP->>BV: getNonSignerStakesAndSignature(signed_batch)
SP->>BV: verifyBlobV2(batch_header, blob_verification_info, nonSignerStakesAndSignature)
SP->>BI: Submit cert = (batch_header, blob_verification_info, nonSignerStakesAndSignature)
%% Validation Flow
V->>BI: Read cert
V->>VP: GET /get/{cert} → cert
activate V
Note over VP: Extract relay_key + blob_header_hash from cert
VP->>R: GetBlob(blob_header_hash)
R-->>VP: Return blob
VP->>BV: verifyBlobV2
VP-->>V: Return validated blob
deactivate V
Ultra High Resolution Diagram
APIs
Below we give a summary of the APIs relevant to understanding the EigenDA high-level diagram

Proxy
See our gorilla/mux routes for full detail, but the gist is that proxy presents a REST endpoint based off of the op da-server spec to rollup batchers:
# OP
POST /put body: <preimage_bytes> → <hex_encoded_commitment>
GET /get/{hex_encoded_commitment} → <preimage_bytes>
# NITRO
Same as OP but add a `?commitment_mode=standard` query param
to both POST and GET methods.
Disperser
The disperser presents a grpc v2 service endpoint
$ EIGENDA_DISPERSER_PREPROD=disperser-preprod-holesky.eigenda.xyz:443
$ grpcurl $EIGENDA_DISPERSER_PREPROD list disperser.v2.Disperser
disperser.v2.Disperser.DisperseBlob
disperser.v2.Disperser.GetBlobStatus
disperser.v2.Disperser.GetPaymentState
Relay
Relays similarly present a grpc service endpoint
$ EIGENDA_RELAY_PREPROD=relay-1-preprod-holesky.eigenda.xyz:443
$ grpcurl $EIGENDA_RELAY_PREPROD list relay.Relay
relay.Relay.GetBlob
relay.Relay.GetChunks
Contracts
Immutable Cert Verifier
The most important contract for rollups integrations is the EigenDACertVerifier, which presents a function to validate DACerts:
/// @notice Check a DA cert's validity
/// @param abiEncodedCert The ABI encoded certificate. Any cert verifier should decode this ABI encoding based on the certificate version.
/// @return status An enum value. Success is always mapped to 1, and other values are errors specific to each CertVerifier.
function checkDACert(bytes calldata abiEncodedCert) external view returns (uint8 status);
/// @notice Returns the EigenDA certificate version. Used off-chain to identify how to encode a certificate for this CertVerifier.
/// @return The EigenDA certificate version.
function certVersion() external view returns (uint8);
Upgradable Router
EigenDACertVerifierRouter acts as an intermediary contract that maintains an internal mapping of activation_block_number -> EigenDACertVerifier. This contract can be used to enable seamless upgrades for new EigenDACertVerifier and provides a way for a rollup to securely introduce custom quorums and/or modify their security thresholds.
/// @notice Returns the address for the active cert verifier at a given reference block number.
/// The reference block number must not be in the future.
function getCertVerifierAt(uint32 referenceBlockNumber) external view returns (address);
/// @notice Check a DA cert's validity
/// @param abiEncodedCert The ABI encoded certificate. Any cert verifier should decode this ABI encoding based on the certificate version.
/// @return status An enum value. Success is always mapped to 1, and other values are errors specific to each CertVerifier.
function checkDACert(bytes calldata abiEncodedCert) external view returns (uint8 status);
Rollup Payload Lifecycle
How is a rollup’s payload (compressed batches of transactions or state transition diffs) encoded and made available on the EigenDA network?
flowchart TD
subgraph Rollups[Rollup Domain]
RS["Rollup Sequencer<br/>[Software System]<br/>Sequences the rollup; submits rollup payloads to EigenDA for data availability"]
RV["Rollup Validator<br/>[Software System]<br/>Runs a derivation pipeline to validate the rollup"]
Payload[("Rollup Payload<br/>[Data]<br/>Batches of tx data or state transition diffs")]
end
%% Standalone proxy
Proxy["Proxy<br/>[Software System]<br/>Bridges domains by encoding/decoding payloads/blobs"]
subgraph EigenDA[Data Availability Domain]
EN["EigenDA Network<br/>[Software System]<br/>Provides decentralized data availability by storing and serving blobs"]
Blob[("Blob<br/>[Data]<br/>Rollup payload encoded into bn254 field element array")]
Cert[("DA Certificate<br/>[Data]<br/>Proof of Data Availability. Used to retrieve and validate blobs.")]
ETH["Ethereum<br/>[Software System]<br/>Stores EigenDA network properties like operator stakes, etc. Also validates DA Certs."]
end
%% Sequencer Flow
RS -->|"(1) Creates"| Payload
Payload -->|"(2) Sent to"| Proxy
Proxy -->|"(3) Encodes into"| Blob
Blob -->|"(4) Dispersed across"| EN
EN -->|"(5) Verifies signatures according to stakes stored on"| ETH
EN -->|"(6) Returns cert"| Proxy
Proxy -->|"(7) Submits"| Cert
Cert -->|"(8) Posted to"| ETH
%% Validator Flow
RV -->|"(9) Reads certificates"| ETH
RV -->|"(10) Retrieve Compressed Batch from Certificate"| Proxy
%% Styling
classDef system fill:#1168bd,stroke:#0b4884,color:white
classDef container fill:#23a,stroke:#178,color:white
classDef data fill:#f9f,stroke:#c6c,color:black
classDef red fill:#916,stroke:#714,color:white
class RS,RV,EN,ETH,S1,Proxy system
class Rollups,EigenDA container
class Batch,Blob,Cert,D1 data
At a high-level, a rollup sequencer needs to make its payload available for download from validators of its network. The EigenDA network makes use of cryptographic concepts such as KZG commitments as fundamental building blocks. Because of this, it can only work with eigenda blobs (hereafter referred to simply as blobs; see technical definition below) of data. The EigenDA proxy is used to bridge the rollup domain (which deals with payloads) and the EigenDA domain (which deals with blobs).
As an example, an op-stack Ethereum rollup’s payload is a compressed batch of txs (called a frame). This frame gets sent to Ethereum to be made available either as a simple tx, or as a 4844 blob (using a blob tx). Using EigenDA instead of Ethereum for data availability works similarly: the payloads are encoded into an eigenda blob and dispersed to the EigenDA network via an EigenDA disperser. The disperser eventually returns a DACert containing signatures of EigenDA operators certifying the availability of the data, which is then posted to Ethereum as the input field of a normal tx. Note that due to the rollup settling on Ethereum, Ethereum DA is needed, but only to make the DACert available, which is much smaller than the blob itself.
Payload: piece of data that an EigenDA client (rollup, avs, etc.) wants to make available. This is typically compressed batches of transactions or state transition diffs.EncodedPayload: payload encoded into a list of bn254 field elements (each 32 bytes), typically with a prefixed field element containing the payload length in bytes, such that the payload can be decoded.PayloadPolynomial: encodedPayload padded with 0s to the next power of 2 (if needed) and interpreted either as evaluations (PolyCoeff) or coefficients (PolyEval) of a polynomial. Because the EigenDA network interprets blobs as coefficients, aPolyEvalwill need to be IFFT’d into aPolyCoeffbefore being dispersed.(EigenDA) Blob: array of bn254 field elements of length a power of two. Interpreted by the network as coefficients of a polynomial. Equivalent toPolyCoeff.Blob Header: contains the information necessary to uniquely identify a BlobDispersal request.Blob Certificate: Signed BlobHeader along with relayKeys, which uniquely identify a relay service for DA Nodes to retrieve chunks from and clients to retrieve full blobs from.Batch: Batch of blobs whose blob certs are aggregated into a merkle tree and dispersed together for better network efficiency.DA Certificate(orDACert): contains the information necessary to retrieve and verify a blob from the EigenDA network, along with a proof of availability.AltDACommitment: RLP serializedDACertprepended with rollup-specific header bytes. This commitment is what gets sent to the rollup’s batcher inbox.
EigenDACertVerifier: contains one main important function checkDACert which is used to verifyDACerts.EigenDACertVerifierRouter: contains router mapping of activation block number toEigenDACertVerifierand allows for securely and deterministically upgrading CertVerification constants (security thresholds and custom quorums) over time.EigenDAThresholdRegistry: contains signature related thresholds and blob→chunks encoding related parameters.EigenDARelayRegistry: contains an Ethereum address and DNS hostname (or IP address) for each registered Relay.EigenDADisperserRegistry: contains an Ethereum address network for each registered Disperser.
- Sequencer:
Encoding: Payload → BlobBlobHeader Construction: Blob → BlobHeaderDispersal: (Blob, BlobHeader) → Certificate- Certificate+Blob
Validation - Unhappy path:
Failoverto EthDA
- Certificate+Blob
Posting: Certificate → Ethereum tx
- Validator (exact reverse of sequencer):
Reading: Ethereum tx → CertificateRetrieval: Certificate → Blob- Certificate+Blob
Validation
- Certificate+Blob
Decoding: Blob → Payload
Data Structs
The diagram below represents the transformation from a rollup payload to the different structs that are allowed to be dispersed.
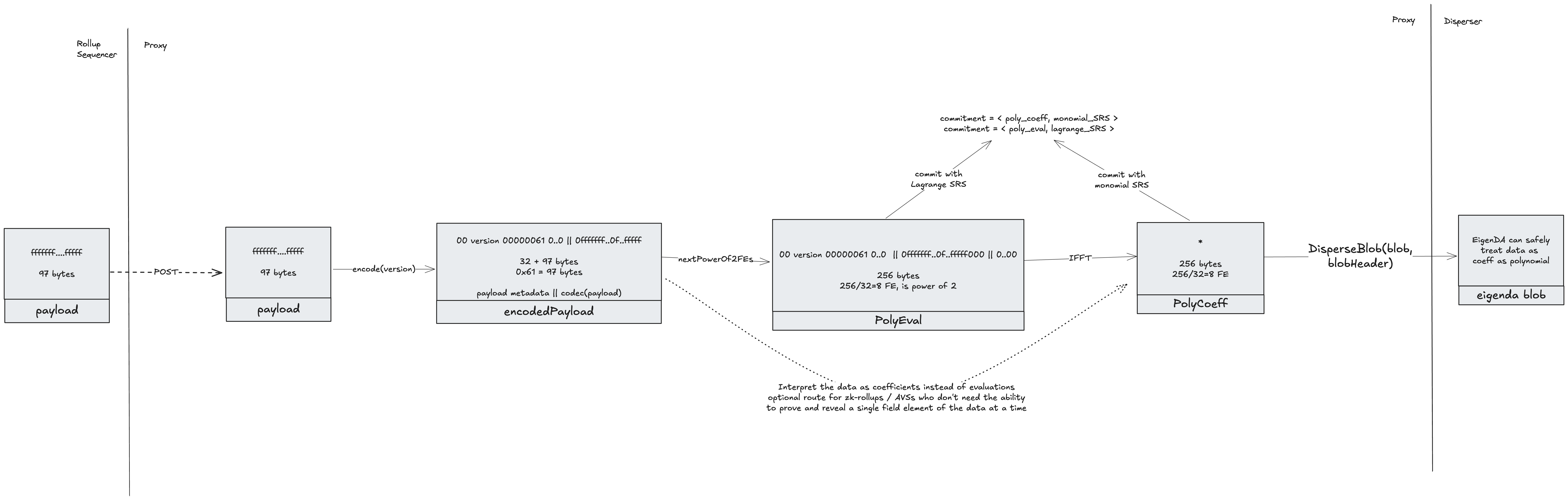
Payload
A client payload is whatever piece of data the EigenDA client wants to make available. For optimistic rollups this would be compressed batches of txs (frames). For (most) zk-rollups this would be compressed state transitions. For AVSs it could be Proofs, or Pictures, or any arbitrary data.
A payload must fit inside an EigenDA blob to be dispersed. See the allowed blob sizes in the Blob section.
EncodedPayload
An encodedPayload is the bn254 encoding of the payload, prefixed with an encoded payload header. It is an intermediary processing artifact, named here for clarity. The encoding obeys the same constraints as EigenDA blobs:
Every 32 bytes of data is interpreted as an integer in big endian format. Each such integer must stay in the valid range to be interpreted as a field element on the bn254 curve. The valid range is 0 <= x < 21888242871839275222246405745257275088548364400416034343698204186575808495617.
Encoded Payload Header
The header carries metadata needed to decode back to the original payload. Because it is included in the encoded payload, it too must be representable as valid field elements. The header currently takes 32 bytes: the first byte is 0x00 (to ensure it forms a valid field element), followed by an encoding version_byte and 4 bytes representing the size of the original payload. The golang payload clients provided in the eigenda repo currently only support encoding version 0x0. The remaining 26 bytes must be zero.
Encoding Payload Version 0x0
Version 0x0 specifies the following transformation from the original payload to a sequence of field element:
- For every 31 bytes of the payload, insert a zero byte to produce a 32-byte value that is a valid field element.
- Further pad the output above so the final length is a multiple of 32 bytes, and comprises a power-of-two number of 32-byte field elements (32, 64, 128, 256, …) to match EigenDA blob sizing. All of the padding must be 0.
[0x00, version_byte, big-endian uint32 len(payload), 0x00, 0x00,...] +
[0x00, payload[0:31], 0x00, payload[32:63],...,
0x00, payload[n:len(payload)], 0x00, ..., 0x00]
For example, the payload hello would be encoded as
[0x00, 0x00, 0x00, 0x00, 0x00, 0x05, 0x00, 0x00,...] +
[0x00, 'h', 'e', 'l', 'l', 'o', 0x00 * 26]
PayloadPolynomial
EigenDA uses KZG commitments, which represent a commitment to a function. Abstractly speaking, we thus need to represent the encodedPayload as a polynomial. We have two choices: either treat the data as the coefficients of a polynomial, or as evaluations of a polynomial. In order to convert between these two representations, we make use of FFTs which require the data to be a power of 2. Thus, PolyEval and PolyCoeff are defined as being an encodedPayload and interpreted as desired.
Once an interpretation of the data has been chosen, one can convert between them as follows:
PolyCoeff --FFT--> PolyEval
PolyCoeff <--IFFT-- PolyEval
Whereas Ethereum treats 4844 blobs as evaluations of a polynomial, EigenDA instead interprets EigenDA blobs as coefficients of a polynomial. Thus, only PolyCoeffs can be submitted as a blob to the Disperser. Each rollup integration must thus decide whether to interpret their encodedPayloads as PolyCoeff, which can directly be dispersed, or as PolyEval, which will require IFFT’ing into a PolyCoeff before being dispersed.
Typically, optimistic rollups will interpret the data as being evaluations. This allows creating point opening proofs to reveal a single field element (32 byte chunk) at a time, which is needed for interactive fraud proofs (e.g. see how optimism fraud proves 4844 blobs). ZK rollups, on the flip side, don't require point opening proofs and thus can safely save on the extra IFFT compute costs and instead interpret their data as coefficients directly.
Blob
A blob is a bn254 field elements array that has a power of 2. It is interpreted by the EigenDA network as containing the coefficients of a polynomial (unlike Ethereum which treats blobs as being evaluations of a polynomial).
An encodedPayload can thus be transformed into a blob directly or optionally by taking IFFT on itself, with size currently limited to 16MiB. There is no minimum size, but any blob smaller than 128KiB will be charged for 128KiB.
BlobHeader
The blobHeader is submitted alongside the blob as part of the DisperseBlob request, and the hash of its ABI encoding (blobKey, also known as blobHeaderHash) serves as a unique identifier for a blob dispersal. This identifier is used to retrieve the blob.
The BlobHeader contains four main sections that must be constructed. It is passed into the DisperseBlobRequest and is signed over for payment authorization.
Refer to the eigenda protobufs for full details of this struct.
Version
The blobHeader version refers to one of the versionedBlobParams structs defined in the EigenDAThresholdRegistry contract.
QuorumNumbers
QuorumNumbers represents a list of quorums required to sign and make the blob available. Quorum 0 represents the ETH quorum, quorum 1 represents the EIGEN quorum — both are always required. Custom quorums can also be added to this list.
BlobCommitment
The BlobCommitment is a binding commitment to an EigenDA Blob. Due to the length field, a BlobCommitment uniquely represents a single Blob. The length field is added to the kzgCommitment to respect the binding property. It is used by the disperser to prove to EigenDA validators that the chunks they received belong to the original blob (or its Reed-Solomon extension).
message BlobCommitment {
// A G1 commitment to the blob data.
bytes commitment = 1;
// A G2 commitment to the blob data.
bytes length_commitment = 2;
// Used with length_commitment to assert the correctness of the `length` field below.
bytes length_proof = 3;
// Length in bn254 field elements (32 bytes) of the blob. Must be a power of 2.
uint32 length = 4;
}
Unlike Ethereum blobs which are all 128KiB, EigenDA blobs can be any power of 2 length between 32KiB and 16MiB (currently), and so the commitment alone is not sufficient to prevent certain attacks:
-
Why is a commitment to the length of the blob necessary?
There are different variants of the attack. The basic invariant the system needs to satisfy is that with the chunks from sufficient set of validators, you can get back the full blob. So the total size of the chunks held by these validators needs to exceed the blob size. If I don't know the blob size (or at least an upper bound), there's no way for the system to validate this invariant. Here’s a simple example. Assume a network of 8 DA nodes, and coding ratio 1/2. For a
blobcontaining 128 field elements (FEs), each node gets 1282/8=32 FEs, meaning that any 4 nodes can join forces and reconstruct the data. Now assume a world without length proof; a malicious disperser receives the same blob, uses the same commitment, but claims that the blob only had length 4 FEs. He sends each node 42/8=1 FE. The chunks submitted to the nodes match the commitment, so the nodes accept and sign over the blob’s batch. But now there are only 8 FEs in the system, which is not enough to reconstruct the original blob (need at least 128 for that).
Note that the length here is the length of the blob (power of 2), which is different from the payload_length encoded as part of the
PayloadHeaderin theblobitself (see the encoding section).
PaymentHeader
The paymentHeader specifies how the blob dispersal to the network will be paid for. There are 2 modes of payment, the permissionless pay-per-blob model and the permissioned reserved-bandwidth approach. See the Payments release doc for full details; we will only describe how to set these 3 fields here.
message PaymentHeader {
// The account ID of the disperser client. This should be a hex-encoded string of the ECDSA public key
// corresponding to the key used by the client to sign the BlobHeader.
string account_id = 1;
// UNIX timestamp in nanoseconds at the time of the dispersal request.
// Used to determine the reservation period, for the reserved-bandwidth payment model.
int64 timestamp = 2;
// Total amount of tokens paid by the requesting account, including the current request.
// Used for the pay-per-blob payment model.
bytes cumulative_payment = 3;
}
Users who want to pay-per-blob need to set the cumulative_payment. timestamp is used by users who have paid for reserved-bandwidth. If both are set, reserved-bandwidth will be used first, and cumulative_payment only used if the entire bandwidth for the current reservation period has been used up.
NOTE: There will be a lot of subtleties added to this logic with the new separate-payment-per-quorum model that is actively being worked on.
An RPC call to the Disperser's GetPaymentState method can be made to query the current state of an account_id. A client can query for this information on startup, cache it, and then update it manually when making dispersals. In this way, it can keep track of its reserved bandwidth usage and current cumulative_payment and set them correctly for subsequent dispersals.
BlobKey (Blob Header Hash)
The blobKey (also known as blob_header_hash or blobHeaderHash) serves as the primary lookup key throughout the EigenDA system. It uniquely identifies a blob dispersal and is used for querying dispersal status, retrieving blobs from the network, and linking blobs to their certificates. The blobKey is computed as the keccak256 hash of the ABI-encoded BlobHeader, and is cryptographically equivalent to the blob_header_hash used in on-chain verification.
Computing the BlobKey
The hashing follows a nested structure. The inner hash covers the blob's content and dispersal requirements (version, quorums, commitment), which is then combined with the payment metadata hash. This ensures that each dispersal request produces a unique blobKey, even when dispersing identical blob content. The disperser enforces this uniqueness; attempting to disperse a blob with a previously used blobKey will result in rejection:
blobKey = keccak256(
abi.encode(
keccak256(abi.encode(blobHeader.version, blobHeader.quorumNumbers, blobHeader.commitment)),
blobHeader.paymentHeaderHash
)
)
Note: The paymentHeaderHash is the keccak256 hash of the PaymentHeader structure (described in the BlobHeader section above). The payment metadata is hashed separately to enable efficient on-chain verification while keeping payment details compact. Additionally, quorumNumbers are sorted in ascending order before hashing to ensure consistency regardless of the order in which quorums are specified.
When a rollup receives an encoded DA commitment from the proxy, the blobKey can be extracted by deserializing the BlobCertificate from the commitment payload, extracting its BlobHeader, and computing the hash as shown above.
In the standard dispersal flow, the disperser computes the blobKey and returns it to the client in the DisperseBlobReply. Clients may independently compute the blobKey for verification purposes or when extracting it from a certificate. The Go and Solidity implementations provided enable both client-side and on-chain computation.
Example
For illustrative purposes, consider a blob dispersal with the following parameters:
version:0x0001quorumNumbers:[0, 1](sorted)commitment: Cryptographic commitment to the blob data (G1 point and G2 length commitment)paymentHeaderHash:0x1234...(32-byte hash of the PaymentHeader)
The blobKey computation proceeds in two steps:
-
Compute inner hash of core dispersal parameters:
innerHash = keccak256(abi.encode(version, quorumNumbers, commitment))This produces a 32-byte hash representing the blob's content and dispersal requirements.
-
Compute outer hash combining inner hash with payment:
blobKey = keccak256(abi.encode(innerHash, paymentHeaderHash))This produces the final 32-byte
blobKey.
The resulting blobKey serves as the unique identifier for querying dispersal status with GetBlobStatus, retrieving chunks from validators via GetChunks, or fetching the full blob from relays via GetBlob.
Relationship to Other Data Structures
The BlobHeader is hashed to produce the blobKey. A BlobCertificate wraps a BlobHeader along with signature and relay keys. The BlobInclusionInfo contains a BlobCertificate and is used to prove inclusion of that certificate in a batch via a Merkle proof. The BatchHeader contains a batchRoot which is the root of the Merkle tree whose leaves are hashes of BlobCertificates. The diagram in the EigenDA Certificate section below illustrates these relationships.
Code References
The Solidity implementation can be found in hashBlobHeaderV2().
The Go implementation is available in ComputeBlobKey().
The EigenDA Go client demonstrates best practices for blobKey verification in verifyReceivedBlobKey(). After receiving a DisperseBlobReply, clients should verify that the disperser didn't modify the BlobHeader by computing the blobKey locally and comparing it with the returned value.
Usage
The blobKey is a central identifier used throughout the dispersal and retrieval process:
-
Dispersal phase: The disperser's
DisperseBlobmethod returns ablobKey. Clients then use thisblobKeywithGetBlobStatusto check when dispersal is complete (see Disperser polling). -
Centralized retrieval: The Relay API's
GetBlobmethod uses theblobKeyas its main lookup parameter to retrieve the full blob from relay servers (see Retrieval Paths). -
Decentralized retrieval: Validators'
GetChunksmethod uses theblobKeyto retrieve erasure-coded chunks directly from validator nodes. Clients can reconstruct the full blob from these chunks (see Retrieval Paths). -
Peripheral APIs: Both the Data API and the Blob Explorer rely on
blobKeyas the primary identifier for querying blob metadata and status. -
Verification: The
blobKeyconnects each blob to its certificate, ensuring that the certificate corresponds to the correct blob.
EigenDA Certificate (DACert)
An EigenDA Certificate (or short DACert) contains all the information needed to retrieve a blob from the EigenDA network, as well as validate it.
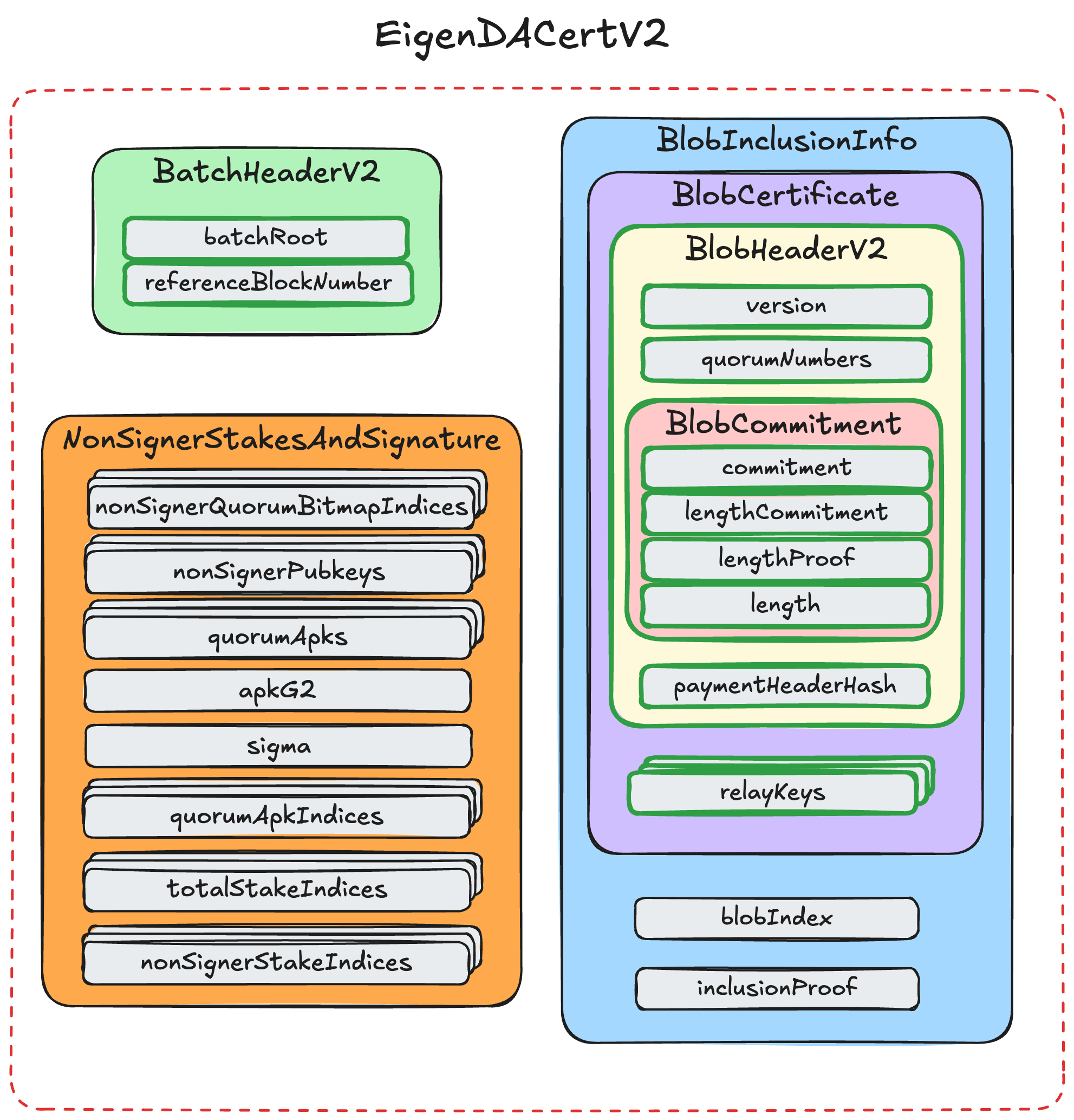
A DACert contains the four data structs needed to call checkDACert on the EigenDACertVerifier.sol contract. Please refer to the eigenda core spec for more details, but in short, the BlobCertificate is included as a leaf inside the merkle tree identified by the batch_root in the BatchHeader. The BlobInclusionInfo contains the information needed to prove this merkle tree inclusion. The NonSignerStakesAndSignature contains the aggregated BLS signature sigma of the EigenDA validators. sigma is a signature over the BatchHeader. The signedQuorumNumbers contains the quorum IDs that DA nodes signed over for the blob.
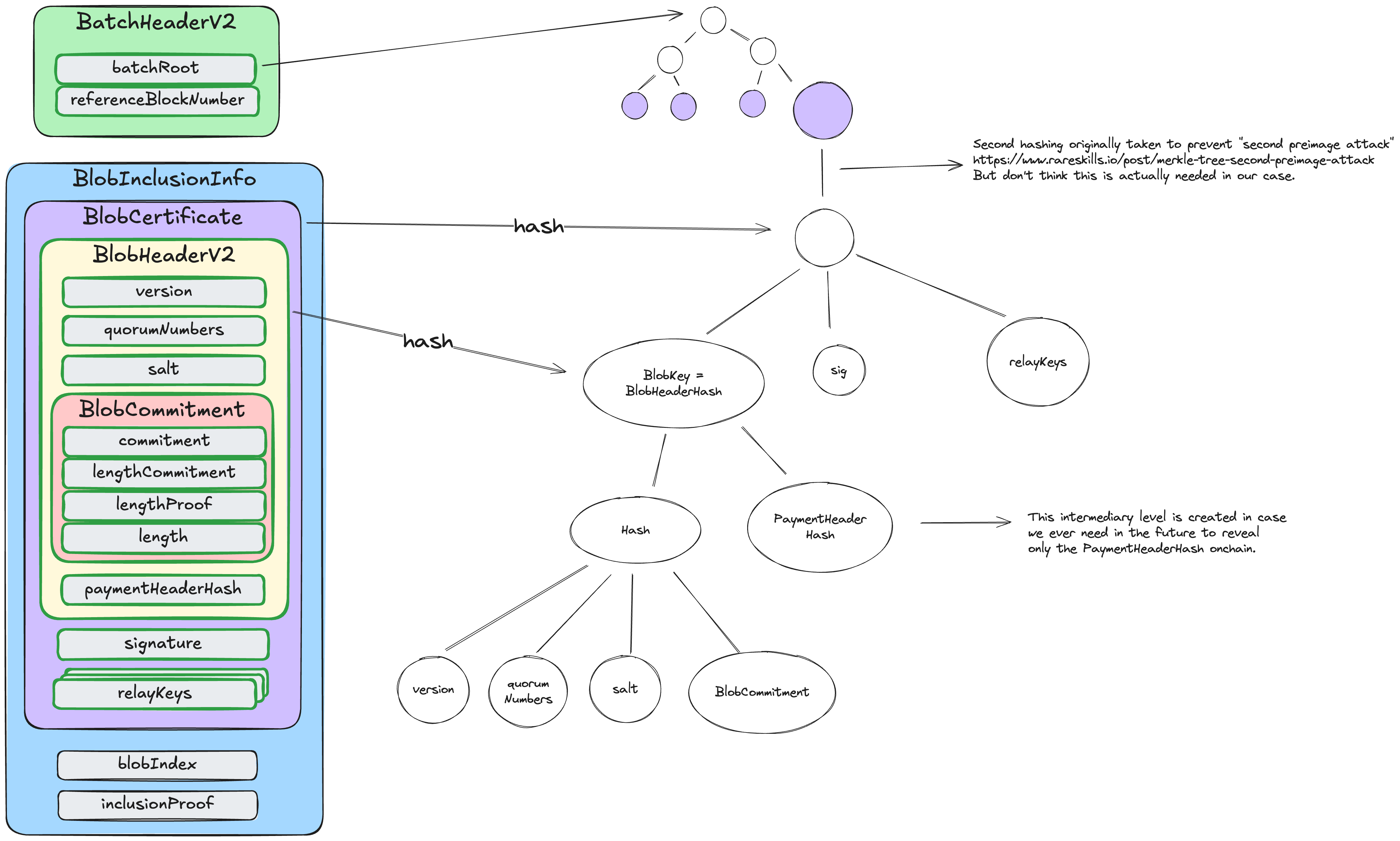
Cert Version
After the Blazer EigenDA network upgrade, three DACert versions exist: V2, V3, and V4. Integrations are expected to use the latest version.
- EigenDACertV2: The diagram displays all the members.
- EigenDACertV3: Defined in the contract. It contains the same members as EigenDACertV2, but with a different ordering:
BatchHeaderV2appears as the first member. - EigenDACertV4: Identical to EigenDACertV3 except for an additional uint16 field named offchainDerivationVersion, appended at the end. See contract.
AltDACommitment
In order to be understood by each rollup stack’s derivation pipeline, the encoded DACert must be prepended with header bytes, to turn it into an altda-commitment respective to each stack:
- op prepends 3 bytes:
version_byte,commitment_type,da_layer_byte - nitro prepends 1 byte:
version_byte
NOTE
In the future we plan to support a custom encoding byte which allows a user to specify different encoding formats for the DACert (e.g, RLP, ABI).
Rollup Managed Contracts
This page describes contracts that are managed by rollups, but are needed to secure the EigenDA integration. For EigenDA-managed core contracts, see the core contracts page.
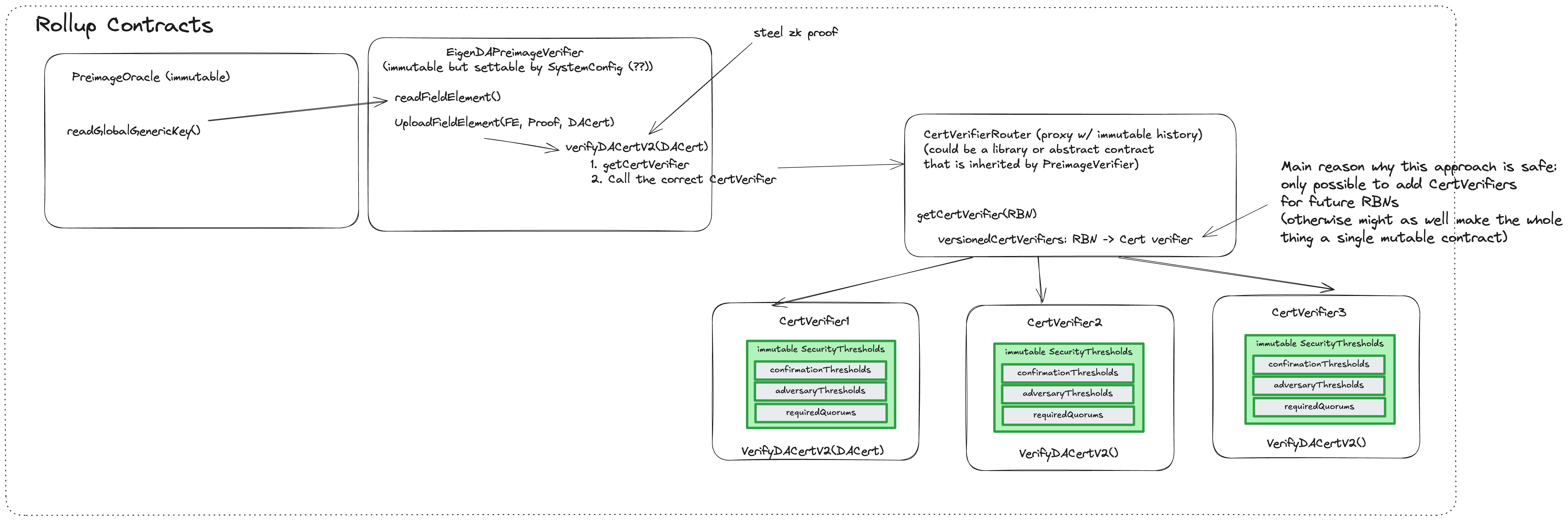
EigenDACertVerifier
This contract's main use case is exposing a function checkDACert which is used to verify DACerts. This function’s logic is described in the Cert Validation section.
The contract also exposes a certVersion method which is called by the payload disperser client to know which cert version to build in order to be verifiable by that contract.
CertVerifier deployment instruction can be found on github.
EigenDACertVerifierRouter
This contract primarily facilitates secure upgrades of EigenDACertVerifier contracts while enabling custom quorum and threshold configurations in a format that maintains cross-version compatibility. This is done through maintaining a stateful mapping:
/// @notice A mapping from an activation block number (ABN) to a cert verifier address.
mapping(uint32 => address) public certVerifiers;
/// @notice The list of Activation Block Numbers (ABNs) for the cert verifiers.
/// @dev The list is guaranteed to be in ascending order
/// and corresponds to the keys of the certVerifiers mapping.
uint32[] public certVerifierABNs;
where each key refers to an activation_block_number (ABN). When calling checkDACert, the reference block number is decoded from the DACert bytes and is used to find the unique CertVerifier active at that RBN (a reverse linear search over the certVerifierABNs is performed). Once found, EigenDACertVerifier at the particular ABN is used for calling checkDACert to verify the DA Cert.
The EigenDACertVerifierRouter enables the use of a certificate’s Reference Block Number (RBN) as a commitment to the specific EigenDACertVerifier that should be used for verification. This mechanism ensures backward compatibility with older DA Certs, allowing an optimistic rollup to continue verifying historical data availability proofs accurately across verifier upgrades.
EigenDACertVerifierRouter deployment instruction can be found on github.
Lifecycle Phases
Secure interaction between a rollup and EigenDA is composed of three distinct system flows:
- Dispersal: Submitting payload data to the DA network
- Retrieval: Fetching payload data from the DA network
- Verification: Ensuring the integrity and quorum-based certification of data availability. Where and how verification is performed is often contingent on how an integration is implemented; e.g:
- Pessimistic Verification where a
DACertis checked as pre-inclusion check for a sequencer inbox - Optimistic Verification where a
DACertis only verified in a worst-case challenge
- Pessimistic Verification where a
Secure Dispersal
Diagram
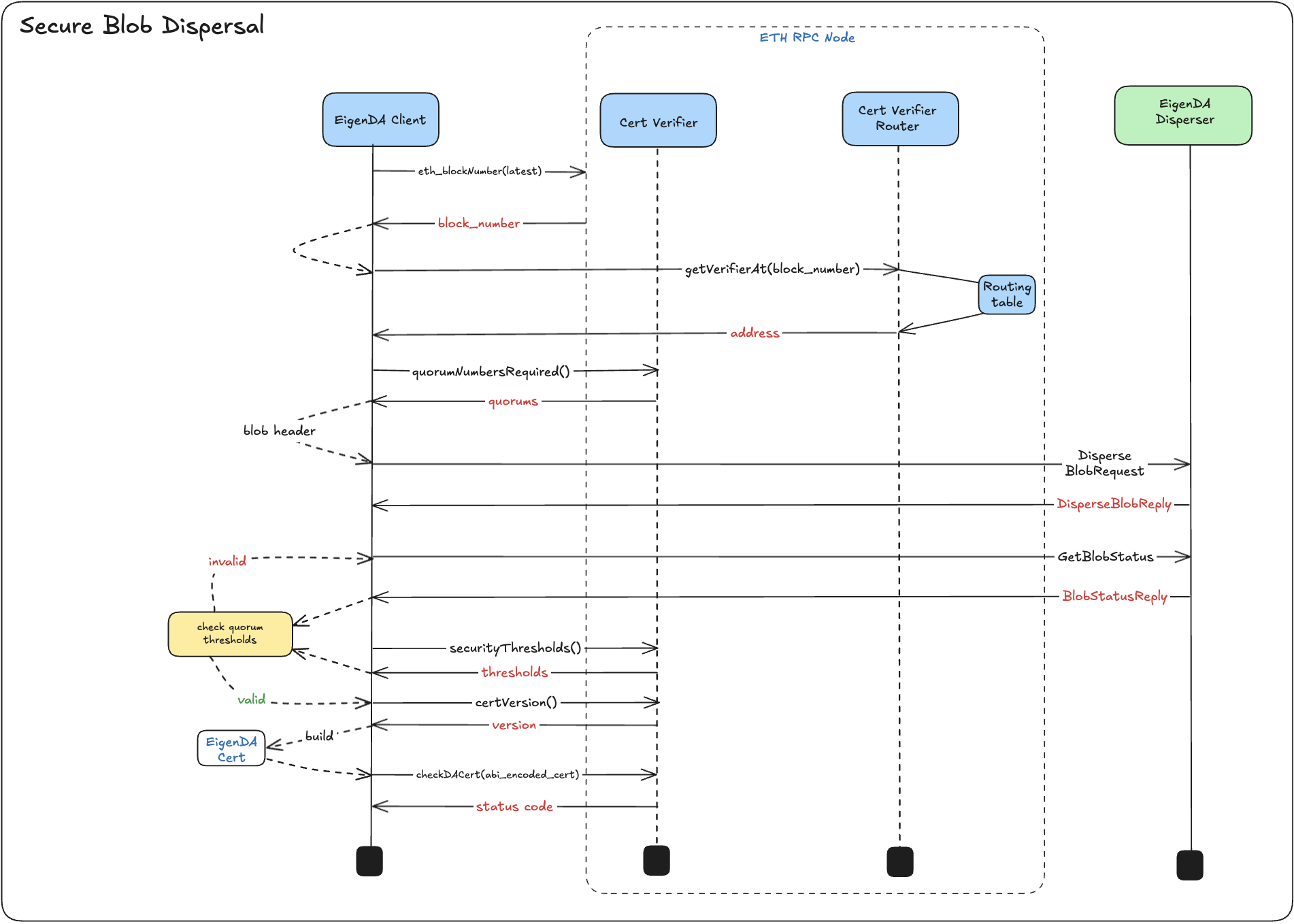
System Flow
-
EigenDA Client takes a raw payload bytes and converts it into a blob.
-
Using
latest_block_number(lbn) number fetched from ETH RPC node, EigenDA Client calls the router to get theEigenDACertVerifiercontract address most likely (if usingEigenDACertVerifierRouter) to be committed to by thereference_block_number(rbn) returned by the EigenDA disperser. -
Using the
verifier, EigenDA Client fetches therequired_quorumsand embeds them into theBlobHeaderas part of the disperser request. -
The EigenDA Client submits the payload blob request to the EigenDA disperser via
DisperseBlobendpoint and polls for aBlobStatusReply(BSR). -
While querying the disperser's
GetBlobStatusendpoint, EigenDA Client periodically checks against the confirmation threshold as it’s updated in real-time by the disperser using the rbn returned in theBlobStatusReplyfor fetching thresholds. (ref) -
Once confirmation thresholds are fulfilled, EigenDA Client calls the
verifier'scertVersion()method to get thecert_versionand casts theDACertinto a structured ABI binding type using thecert_versionto dictate which certificate representation to use. (ref) -
EigenDA Client then passes ABI encoded cert bytes via a call to the
verifier'scheckDACertfunction which performs onchain cert verification logic and returns a uintverification_status_code -
Using the
verification_status_code, the EigenDA Client determines whether to:- Return the certificate (i.e.,
CertV2Lib.StatusCode.SUCCESS) to the Rollup Batcher, or - Failover if any other status code is returned.
- Return the certificate (i.e.,
Payload to Blob Encoding
This phase occurs inside the eigenda-proxy, because the proxy acts as the “bridge” between the Rollup Domain and Data Availability Domain (see lifecycle diagram).
A payload consists of an arbitrary byte array. The DisperseBlob endpoint accepts a blob, which needs to be an encoded bn254 field element array.
Disperser polling
The DisperseBlob method takes a blob and blob_header as input. The hash of the blob_header (known as the blobKey) serves as a unique identifier for tracking the dispersal status. Under the hood, the disperser performs the following steps:
- Batching: The blob is aggregated into a Merkle tree along with other blobs.
- Reed-Solomon Encoding: The blob is erasure-coded into chunks for fault tolerance.
- Dispersal to Validators: The chunks are distributed to EigenDA validator nodes based on the required quorum settings.
- Signature Collection: The disperser collects BLS signatures from participating validators.
- Status Reporting: A
BlobStatusReplyis returned to the client to reflect progress or terminal status.
The disperser batches blobs for a few seconds before dispersing them to nodes, so an entire dispersal process can exceed 10 seconds. For this reason, the API has been designed asynchronously with 2 relevant methods.
// Async call which queues up the blob for processing and immediately returns.
rpc DisperseBlob(DisperseBlobRequest) returns (DisperseBlobReply) {}
// Polled for the blob status updates, until a terminal status is received
rpc GetBlobStatus(BlobStatusRequest) returns (BlobStatusReply) {}
// Intermediate states: QUEUED, ENCODED, GATHERING_SIGNATURES
// Terminal states: UNKNOWN, COMPLETE, FAILED
enum BlobStatus {
UNKNOWN = 0; // functionally equivalent to FAILED but for unknown unknown bugs
QUEUED = 1; // Initial state after a DisperseBlob call returns
ENCODED = 2; // Reed-Solomon encoded into chunks ready to be dispersed to DA Nodes
GATHERING_SIGNATURES = 3; // blob chunks are actively being transmitted to validators
COMPLETE = 4; // blob has been dispersed and attested by DA nodes
FAILED = 5;
}
After a successful DisperseBlob RPC call, the disperser returns BlobStatus.QUEUED. To retrieve a valid BlobStatusResponse, the GetBlobStatus RPC endpoint should be polled until a terminal status is reached.
If BlobStatus.GATHERING_SIGNATURES is returned, the signed_batch and blob_verification_info fields will be present in the BlobStatusReply. These can be used to construct a DACert, which may be verified immediately against the configured threshold parameters stored in the EigenDACertVerifier contract. If the verification passes, the certificate can be accepted early. If verification fails, polling should continue.
Once BlobStatus.COMPLETE is returned, it indicates that the disperser has stopped collecting additional signatures, typically due to reaching a timeout or encountering an issue. While the signed_batch and blob_verification_info fields will be populated and can be used to construct a DACert, the DACert could still be invalid if an insufficient amount of signatures were collected in-regards to the threshold parameters.
Any other terminal status indicates failure, and a new blob dispersal will need to be made.
Failover to Native Rollup DA
Proxy can be configured to retry BlobStatus.UNKNOWN, BlobStatus.FAILED, & BlobStatus.COMPLETE (if threshold check failed) dispersal n times, after which it returns to the rollup a 503 HTTP status code which rollup batchers can use to failover to EthDA or native rollup DA offerings (e.g, arbitrum anytrust).
The Proxy will return a 503 Service Unavailable status code in cases where a dispersal succeeds against the Disperser but verification fails against the EigenDACertVerifier contract (i.e, any status code != SUCCESS).
See here for more info on the OP implementation and here for Arbitrum.
BlobStatusReply → Cert
Implementation Note: While not mandated by the EigenDA spec, clients must currently reconstruct the
DACertfrom fields in theBlobStatusReply, as the disperser does not return a cert directly. The transformation is visualized in the Ultra High Res Diagram.
In the updated implementation, a CertBuilder constructs the DA Cert through direct communication with the OperatorStateRetriever contract, which provides the necessary information about operator stake states. This approach ensures accurate on-chain data for certificate verification. The following pseudocode demonstrates this process:
class DACert:
batch_header: any
blob_verification_proof: any
nonsigner_stake_sigs: any
cert_version: uint8
signedQuorumNumbers: bytes
def get_da_cert(blob_header_hash, operator_state_retriever, cert_version_uint8) -> DACert:
"""
DA Cert construction pseudocode with OperatorStateRetriever
@param blob_header_hash: key used for referencing blob status from disperser
@param operator_state_retriever: ABI contract binding for retrieving operator state data
@param cert_version_uint8: uint8 version of the certificate format to use
@return DACert: EigenDA certificate used by rollup
"""
# Call the disperser for the info needed to construct the cert
blob_status_reply = disperser_client.get_blob_status(blob_header_hash)
# Validate the blob_header received, since it uniquely identifies
# an EigenDA dispersal.
blob_header_hash_from_reply = blob_status_reply.blob_verification_info.blob_certificate.blob_header.Hash()
if blob_header_hash \!= blob_header_hash_from_reply:
throw/raise/panic
# Extract first 2 cert fields from blob status reply
batch_header = blob_status_reply.signed_batch.batch_header
blob_verification_proof = blob_status_reply.blob_verification_info
# Get the reference block number from the batch header
reference_block_number = batch_header.reference_block_number
# Get quorum IDs from the blob header
quorum_numbers = blob_verification_info.blob_certificate.blob_header.quorum_numbers
# Retrieve operator state data directly from the OperatorStateRetriever contract
operator_states = operator_state_retriever.getOperatorState(
reference_block_number,
quorum_numbers,
blob_status_reply.signed_batch.signatures
)
# Construct NonSignerStakesAndSignature using the operator state data
nonsigner_stake_sigs = construct_nonsigner_stakes_and_signature(
operator_states,
blob_status_reply.signed_batch.signatures
)
signed_quorum_numbers = blob_status_reply.signed_batch.quorum_numbers
return DACert(batch_header, blob_verification_proof, nonsigner_stake_sigs, cert_version_uint8, signed_quorum_numbers)
Secure Retrieval
System Diagram
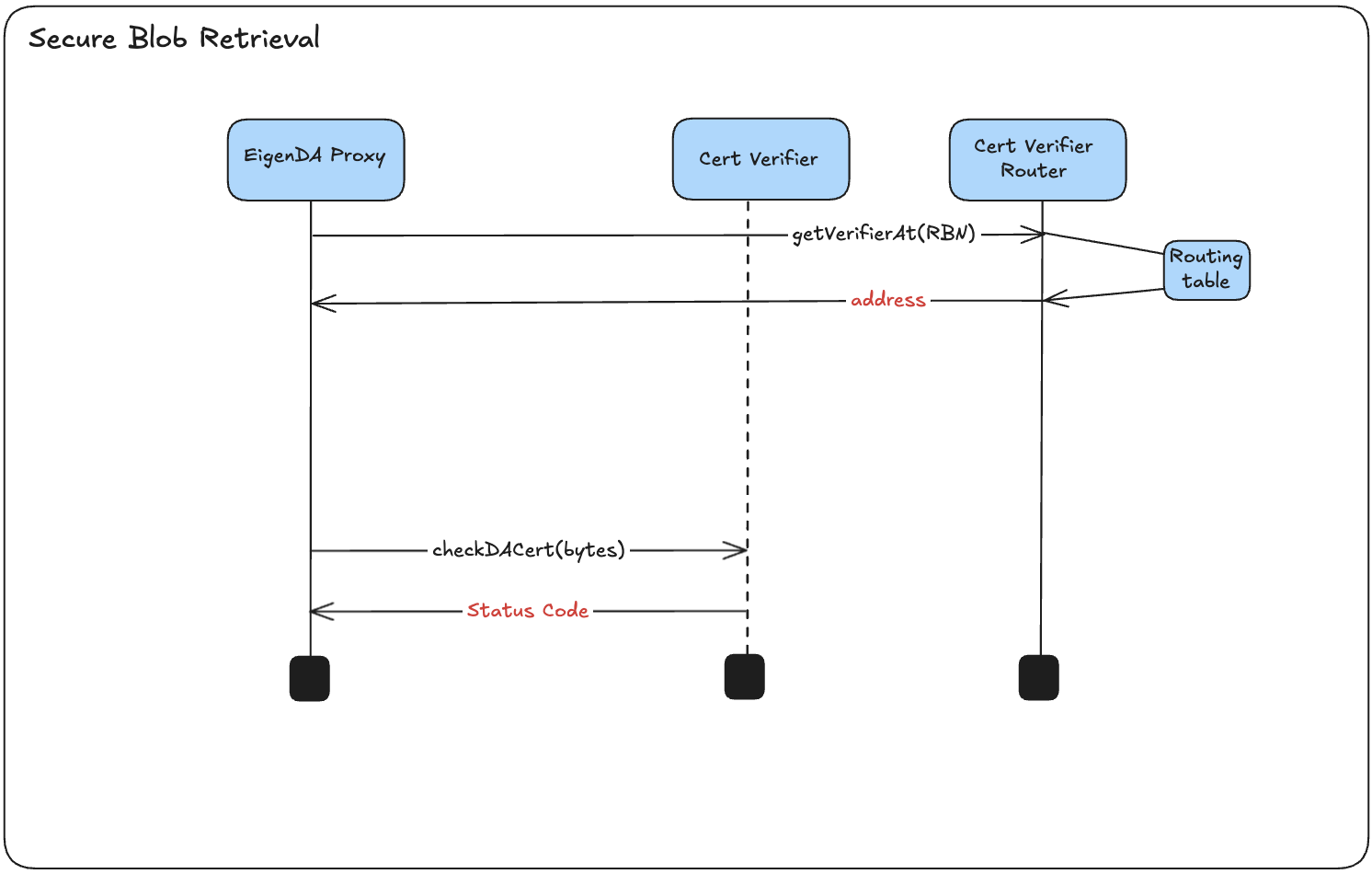
System Flow
-
A Rollup Node queries Proxy’s
/getendpoint to fetch batch contents associated with an encoded DA commitment. -
Proxy decodes the
cert_versionfor the DA commitment and uses an internal mapping ofcert_version⇒cert_abi_structto deserialize into the structured binding cert type. -
Proxy submits ABI encoded cert bytes to
EigenDACertVerifierread call via thecheckDAcertmethod, which returns averification_status_code. -
Proxy interprets the
verification_status_codeto understand how to acknowledge the certificate's validity. If the verification fails, Proxy returns an HTTP 418 I'm a teapot status code, indicating to a secure rollup that it should disregard the certificate and treat it as an empty batch in its derivation pipeline. -
Assuming a valid certificate, Proxy attempts to query EigenDA retrieval paths for the underlying blob contents.
-
Once fetched, Proxy verifies the blob's KZG commitments to ensure tamper resistance (i.e., confirming that what's returned from EigenDA matches what was committed to during dispersal).
-
Proxy decodes the underlying blob into a
payloadtype, which is returned to the Rollup Node.
Retrieval Paths
There are two main blob retrieval paths:
- decentralized retrieval: retrieve erasure coded chunks from Validators and recreate the
blobfrom them. - centralized retrieval: the same Relay API that Validators use to download chunks, can also be used to retrieve full blobs.
EigenDA V2 has a new Relay API for retrieving blobs from the disperser. The GetBlob method takes a blob_key as input, which is the blobKey (also known as blob_header_hash) computed from the BlobHeader. Note that BlobCertificate (different from DACert) contains an array of relay_keys, which are the relays that can serve that specific blob. A relay's URL can be retrieved from the relayKeyToUrl function on the EigenDARelayRegistry.sol contract.
Decoding
Decoding performs the exact reverse operations that Encoding did.
Secure Integration
Audience: This page is for EigenDA and rollup developers implementing secure integrations. For a high-level overview, see our secure integration overview.
Overview
A secure integration must handle malicious data posted on Ethereum L1, unlike trusted integrations. Potential threats include:
- Malicious batcher: Posts invalid or malformed DA certificates (DA Cert)
- Malicious proposer: Publishes incorrect L2 state roots
EigenDA Blob Derivation
This section describes the canonical procedure for deriving a rollup payload from a DA Certificate. This derivation is integral to rollup consensus and must be integrated in both rollup nodes and the proof system in secure integrations.
Current Implementations
- EigenDA Proxy
- OP EigenDA Secure Integration (Hokulea)
Derivation Process
The diagram below shows the step-by-step transformation from input to final rollup payload:
Key Components:
- Input: Serialized DA Cert (as calldata) + block number of DA Cert inclusion
- Blob Derivation: Routes DA cert through validation to one of several terminal states
- Preimage Oracle: Interface for fetching additional data during derivation
- Implementation varies by requirement (e.g., key-value mapping for optimistic fault proofs)
- Host: Entity that provides preimage oracle responses
An encoded payload is an intermediate artifact between the rollup payload and the EigenDA blob. See its definition.
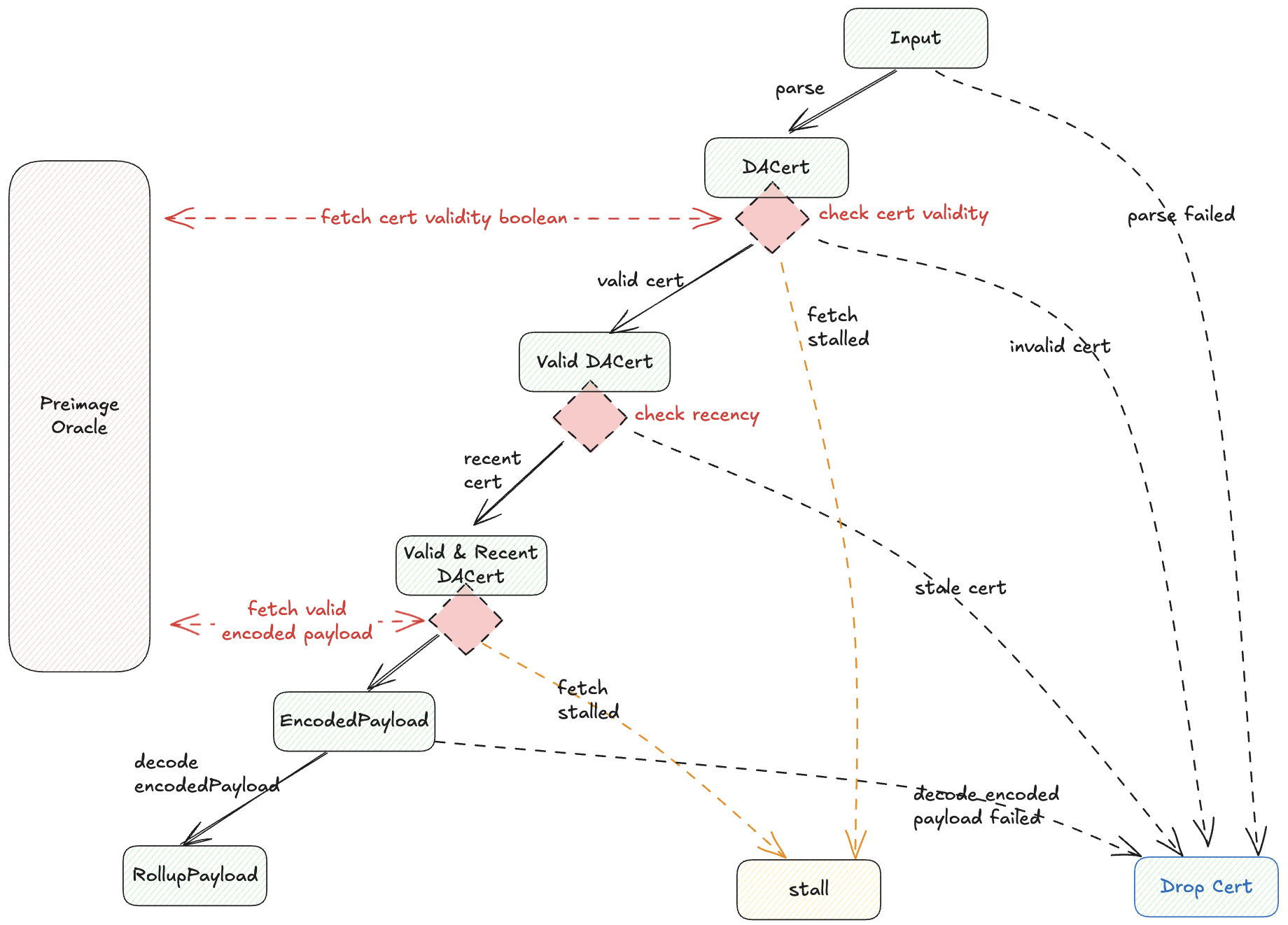
Terminal States
All inputs to the EigenDA derivation pipeline end in exactly one of these states:
| State | Description |
|---|---|
| Dropped | Input rejected and ignored by rollup execution |
| Stalled | Required preimage data unavailable at the moment, and it should be retried |
| Rollup Payload | ✅ Success - desired payload bytes produced |
Failure Cases
When validation fails, the DA Cert is discarded and nothing is forwarded downstream:
Parse Failed
- Batcher submitted improperly-serialized or unrecognized DA Cert
Recency Check Failed
- DA Cert reached rollup inbox after reference block number + recency window
- Host provides false recency window size that leads to failure
Cert Validity Check Failed
- DA Cert doesn't satisfy quorum-attestation constraint or the
offchain derivation versionin the DA Cert differs from the immutable one stored in theEigenDACertVerifier's bytecode. For more information, see upgrade. - Host provides false validity information via preimage oracle
Decode Blob Failed
- EigenDA blob cannot be decoded back to rollup payload per spec
- Causes:
- Host or Batcher intentionally corrupts encoding
Success: If no failures occur, the pipeline outputs the expected payload.
Secure Integration Framework
Rollup consensus must cover all aspects of EigenDA blob derivation. Designers have two degrees of freedom:
- Derivation Split: Choose which parts are executed on-chain (pessimistically via native execution) vs secured off-chain (via proving system)
- Proving VM Choice: Select the on-chain proving virtual machine
Each integration can be tailored to fit specific rollup protocol constraints.
Splitting EigenDA Blob Derivation
Rollups can split the derivation pipeline between on-chain execution and off-chain verification which is secured by some proof system. This degree of freedom allows for variants of integrations that tailored to individual stacks. For examples,
- Arbitrum with EigenDA V1: All components through cert validity checked in rollup inbox
- OP Optimistic Fault Proof Integration: Entire EigenDA blob derivation executes off-chain, and they are secured by the OP FPVM proof system.
Securely integrating with any VM
In order to secure parts from the EigenDA blob derivation taking place off-chain:
- Integration Required: Blob derivation must be imported into L2 consensus as a library
- Compilation: The library compiles to instructions replayable by on-chain VM
- Security: Off-chain derivation secured by proof system
- Complete Coverage: The combined on-chain (pessimistic native execution) and off-chain logics covers entire derivation
Preimage Oracle Requirement: Both on-chain and off-chain implementations needed.
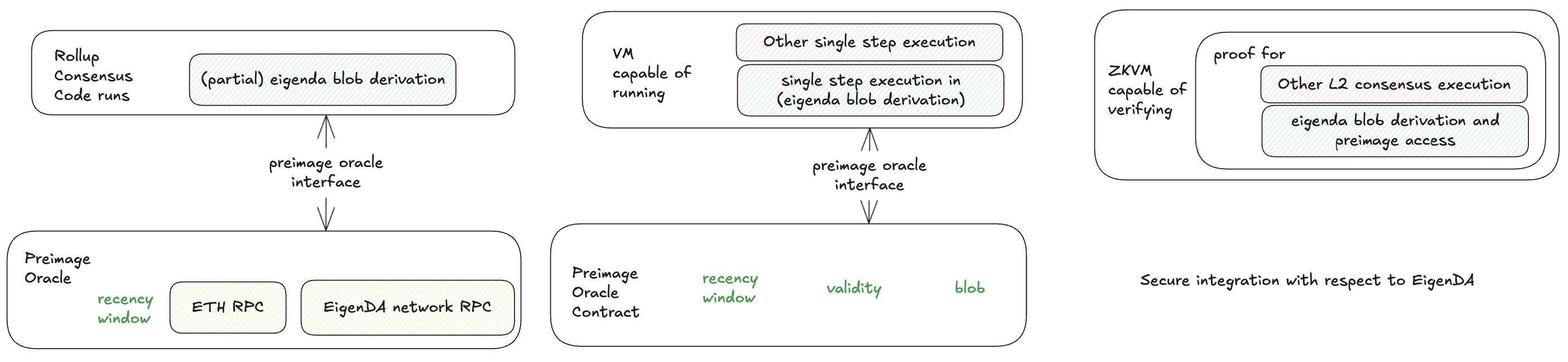
Secure integration with ZKVM
The ZKVM integration must also satisfy the requirements described above. Using a ZKVM can also eliminate the need for pessimistic on-chain execution, but more importantly it allows the system to either act as a ZK rollup or as a standard optimistic rollup that relies on a challenge mechanism.
- ZK rollup integration: Every time the L2 state is updated to L1, a ZK proof must accompany it, covering all state changes since the previous valid update.
- Optimistic ZK fault‑proof integration: Functionally identical to the standard Optimistic Fault‑Proof integration, except the proof system runs on the ZKVM.
EigenDA Blob Derivation in EigenDA Proxy
We have dedicated pages for secure integrations, but let's review the EigenDA Proxy GET path implementation, which has been used in rollup consensus nodes since EigenDA integration began. Proxy also implements WRITE path, solely used by rollup batcher for rollup liveness.
Proxy Architecture for Blob Derivation
The proxy combines:
- Blob derivation logic
- Retrieval clients for preimage data
- Cert validity: ETH RPC
- EigenDA blob: gRPC connection to EigenDA network
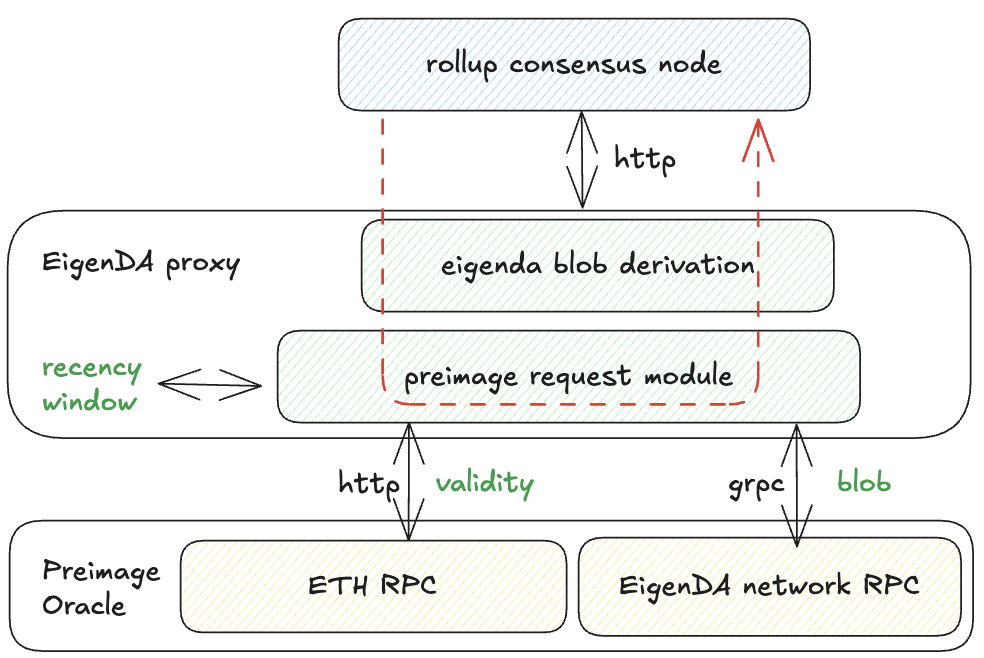
Derivation validation In Depth
1. RBN Recency Validation
This check enforces timing guarantees: once a cert lands in the batcher inbox, optimistic and zk rollup validators must have enough time to download the EigenDA blob.
We use fault proofs to motivate the need for a recency check. A similar reason exists for zk rollup, where the validator of zk rollup must be able to download the EigenDA blob after the rollup prover posts the L2 state update on L1.

From the timeline above, EigenDA’s availability window must overlap the ~7-day challenge period so any honest party can detect faults and fetch the required data. Rollup derivation pipelines should reject certificates whose DA window began too far in the past. While a DA cert doesn’t record its signing or availability time, it does include cert.RBN, which is the L1 Reference Block Number chosen by the disperser to anchor the operator set and stakes. Because RBN is fixed before validators sign, it provides a proxy to bound how old the cert can be at inclusion, enabling a simple recency check.
certL1InclusionBlock - cert.RBN <= RecencyWindowSize
If the inequality fails, discard the cert. This also hardens security by preventing a disperser from choosing a very old RBN with materially different stakes (e.g., after withdrawals).
To give a concrete example with a rollup stack, optimism has a sequencerWindow which forces batches to land onchain in a timely fashion (12h). This filtering however, happens in the BatchQueue stage of the derivation pipeline (DP). But because EigenDA blob derivation needs to take place right after L1Retrieval and before [BatchQueue], we cannot use the OP's existing mechanism in [BatchQueue] with [sequencerWindow] to discard old DA certificate. To prevent this, we need the recencyWindow filtering to happen during the L1Retrieval stage of the DP.
Despite its semantics being slightly different, sequencerWindow and recencyWindow are related concepts, and in order to not force another config change on op altda forks, we suggest using the same value as the
SequencerWindowSizefor theRecencyWindowSize, namely 12h.
For the ~7-day challenge window overlaps EigenDA availability, we assume there is at least one honest challenger runs an L2 consensus node and downloads the EigenDA blob soon after the batch is posted on L1. Define L2StatePostingPeriod as the interval between (a) L1 inclusion of the certificate in the batcher inbox and (b) L1 inclusion of the corresponding L2 state update. As long as L2StatePostingPeriod + RecencyWindowSize < ~7 days, the honest challenger can deter any invalid-proposal attack.
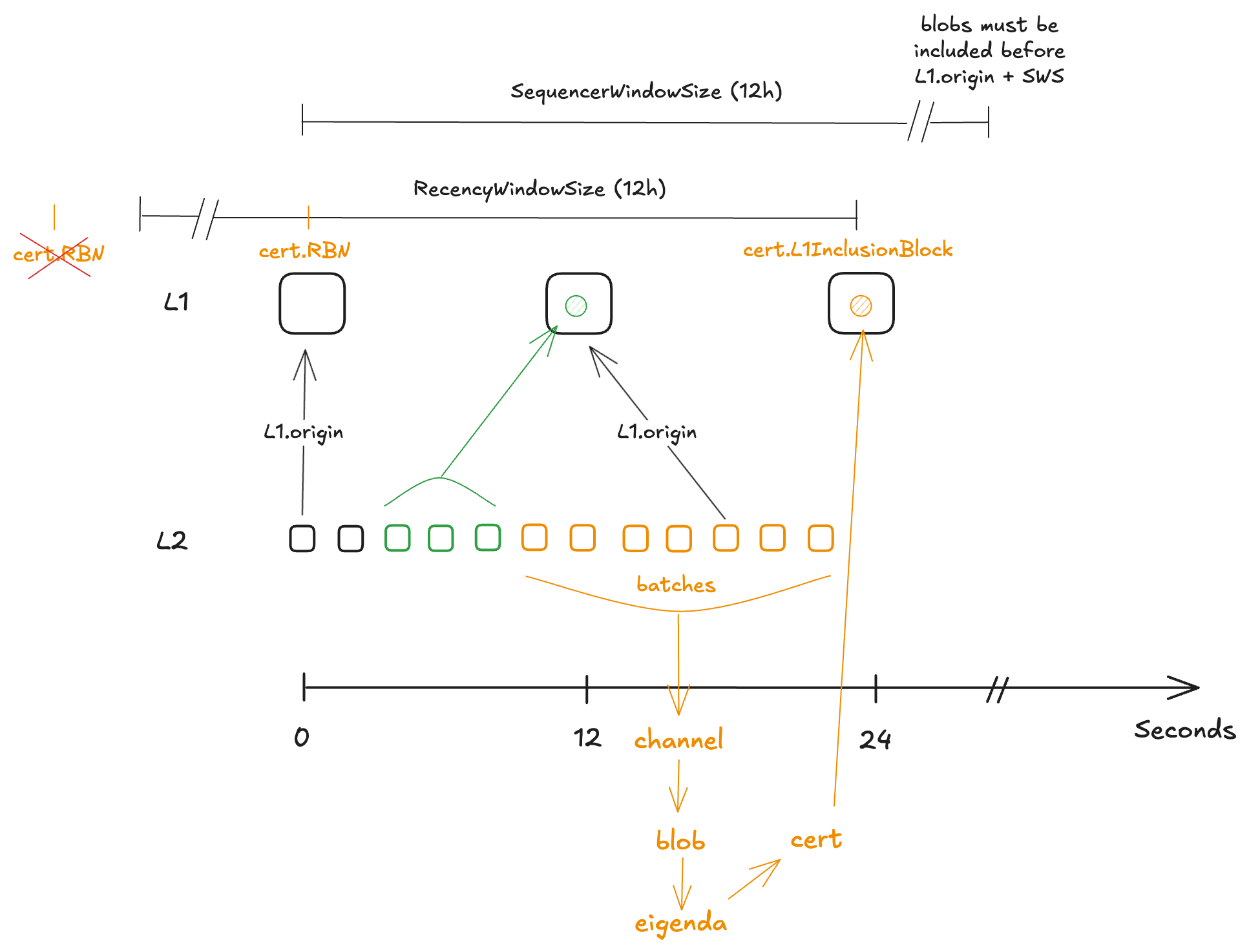
In the diagram, the top row shows L1 blocks every 12 s; the smaller squares are L2 blocks every 2 s. Yellow labels mark key artifacts across the batching pipeline: batches → channel → EigenDA blob. Dispersal completes between t=12 s and t=24 s. The resulting certificate has RBN equal to the L1 block at t=0 (two L1 blocks earlier). The cert is then submitted to L1 at t=24 s. Green annotations show the generalized L2→L1 submission, with batches posted to the adjacent L1 block.
Exception
However, if the RecencyWindowSize is configured to be 0, the entire recency check is skipped. It is strongly not recommended to set it to 0, as it allows a malicious or misbehaving batcher to submit an AltDACommitment whose blob has been pruned by the DA network. An altda commitments is considered valid and can be processed by the next stage of the eigenda blob derivation.
Protocol controlled recency window size
The RecencyWindowSize is determined by offchainDerivationVersion if the integration uses a DA Cert with version >= 4. For offchainDerivationVersion=0, the RecencyWindowSize is 14400 measured in number of Ethereum blocks (assuming 12 second block production time), roughly corresponding to 48 hours. Any DA Cert before V4 isn't checked for recency (i.e,RecencyWindowSize=0) since there's no offchainDerivationVersion field present in the legacy DA Certs.
2. Cert Validation
Cert validation is done inside the EigenDACertVerifier contract, which EigenDA deploys as-is, but is also available for rollups to modify and deploy on their own. Specifically, checkDACert is the entry point for validation. This could either be called during a normal eth transaction (either for pessimistic “bridging” like EigenDA V1 used to do, or when uploading a Blob Field Element to a one-step-proof’s preimage contract), or be zk proven using a library like Steel and Sp1CC.
The checkDACert function accepts an ABI-encoded []byte certificate input. This design allows the underlying DACert structure to evolve across versions, enabling seamless upgrades without requiring changes to the EigenDACertVerifierRouter interface.
The checkDACert function is implemented using a non-revertable pattern.
This is done to ensure both liveness and safety for a rollup's proof generation/verification flow; ie:
- Steel proofs for
eth_callsimulations that revert result in a stark execution proof failing to generate - Optimistic fraud proofs like Arbitrum BoLD's proving system expect that an invalid DA Cert can be provably invalid. A one step proof tx reverting could result in an challenger forced to forfeit their bond. Rather than allowing Solidity reverts or EVM exceptions to propagate, all error conditions are captured and mapped into explicit status codes.
Status Codes
The EigenDACertVerifier contract maintains three status codes that define rollup posting and derivation behavior:
-
SUCCESS
Indicates that the DA Certificate fulfills all correctness guarantees.
Rollup batch posting and derivation may proceed safely. -
INTERNAL_ERROR
Represents Solidity compiler-level or EVM exception errors, including but not limited to:- Arithmetic overflow or underflow.
- Out-of-gas or invalid opcode execution.
- Any Solidity compiler-injected runtime error.
-
INVALID_CERT
Indicates that the DA Cert violates critical invariants. This implies an invalid or insecure certificate, and rollup posting must not proceed and derivation must treat the associated Rollup Payload as an empty batch.
The cert verification logic consists of:
- verify blob batch merkleInclusion proof
- verify
sigma(operators’ bls signature) overbatchRootusing theNonSignerStakesAndSignaturestruct - verify blob security params (blob_params + security thresholds)
- verify each quorum part of the blob_header has met its threshold
- verify equality between
offchainDerivationVersionpresent in the DA Cert andoffchainDerivationVersionthat's hardcoded in theEigenDACertVerifier
More information about upgrading the cert verification can be found in the section.
3. Downloading and Decoding an Encoded Payload
Downloading an Encoded Payload
The preimage oracle served encoded payload. When the EigenDA blob derivation queries the preimage oracle for the encoded payload corresponding to a DA cert, the preimage oracle (i.e. the preimage request module of the EigenDA proxy) downloads the EigenDA blob from relay or directly from EigenDA operators, or any data sources including pre-populated local storage or s3 that stores the EigenDA blob. The preimage oracle performs checks on the blob against the KZG commitment from the DA cert. If verification fails, it discards the blob and retries with other sources until a valid one is found. Once verified, it returns the encoded payload to the derivation step.
A rollup may apply an FFT on the blob to obtain its encoded payload, or use the blob directly as the encoded payload, depending on whether an inverse FFT was taken on the encoded payload during the dispersal path. Taking IFFT on the dispersal path lets the rollup open points on bytes using parts of the payload. Both Arbitrum Nitro and OP (optimistic or ZK) apply IFFT. The encoded payload always live in the same domain (i.e. without any data transformation) as the payload. It is formed by adding the encoded payload header and interleaving 0s to make every 32bytes a valid field element, the padding 0s at the end to a power of two number of field elements (each 32 bytes).
Decoding an Encoded Payload
After verification, EigenDA blob derivation decodes the encoded payload to the original rollup payload. If any check fails, discard the blob returned from the preimage oracle. The procedure:
- checkLenInvariant
- Encoded payload size ≥ size of encoded payload header.
- Encoded payload contains a power-of-two number of 32-byte field elements (valid sizes: 32, 64, 128, 256, …). See client implementation.
- decodeHeader: (first 32-byte field element)
- Encoded payload size ≥ size of encoded payload header.
- First byte is 0x00 so the first 32 bytes form a valid field element.
- Encoding version is known (currently 0x00).
- Returns the claimed original rollup payload size.
- decodePayload
- Remove internal padding (drop the first byte of each 32-byte word).
- Decoded size must be ≥ the claimed length.
The EigenDA protocol enforces blob length > 0 (see implementation).
Proxy behavior. The EigenDA proxy can return either the encoded payload or the decoded rollup payload based on GET parameters:
- With
?return_encoded_payload=trueor?return_encoded_payload=1, it only checks the blob against the kzg commitment and returns the encoded payload, it is useful when integrating with proof systems to control the data transformation. - Without parameters, it decodes and returns the rollup payload; on any decoding error, it returns HTTP 418.
Upgradable Quorums and Thresholds for Optimistic Verification
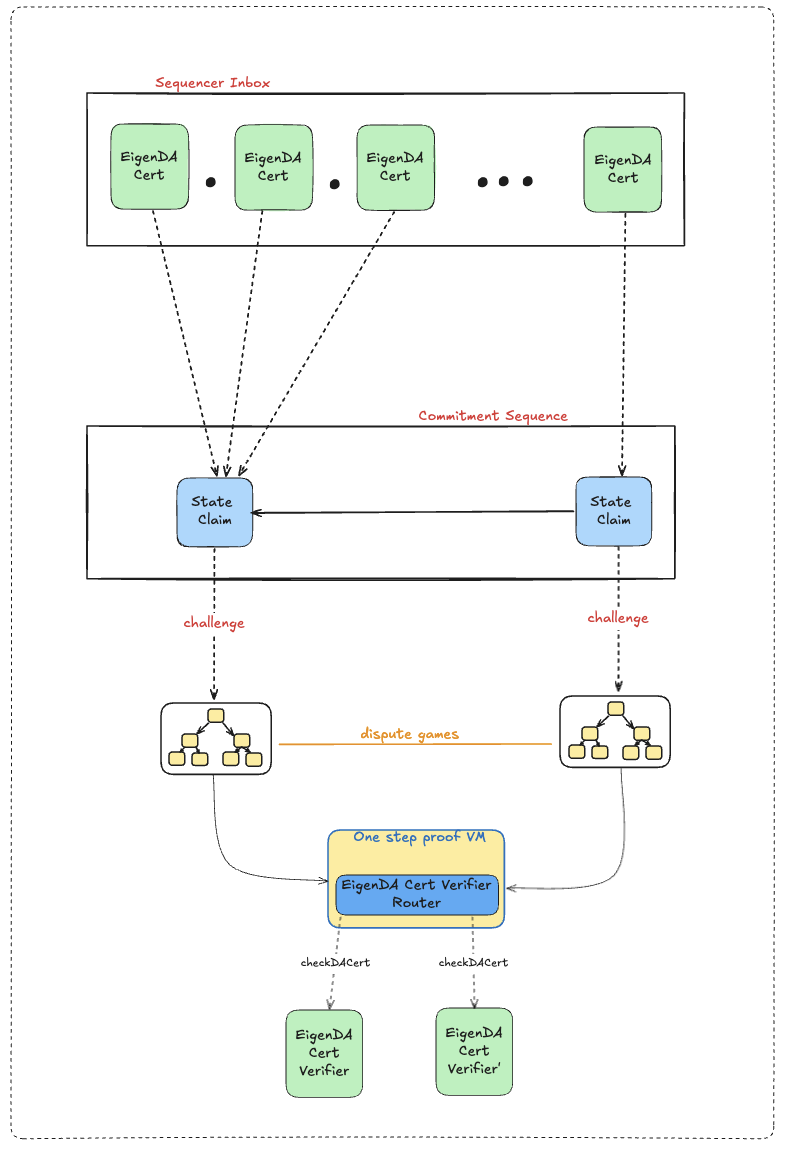
The EigenDACertVerifierRouter contract enables secure upgrades to a rollup’s required quorums and thresholds without compromising the integrity of previously submitted state commitments. It achieves this by routing certificate verification to the appropriate EigenDACertVerifier instance based on the reference_block_number embedded in the cert, which dictates the verifier whose activation block was effective at that time. This ensures backward compatibility, allowing older DACerts to be validated against the verifier version that was active at the time of their creation.
The router is typically deployed behind an upgradable admin proxy and should use the same ProxyAdmin multisig as the rollup for consistent and secure access control.
Adding New Verifiers — Synchronization Risk
There is a synchronization risk that can temporarily cause dispersals to fail when adding a new verifier' to the EigenDACertVerifierRouter at a future activation block number (abn'). If latest_block < abn' and rbn >= abn', dispersals may fail if the required_quorums set differs between verifier and verifier'. In this case, the quorums included in the client's BlobHeader (based on the old verifier) would not match those expected by checkDACert (using the new verifier). This mismatch results in at most a few failed dispersals, which will resolve once latest_block >= abn' and reference_block_number >= abn', ensuring verifier consistency. The EigenDA integrations team will explore mitigations in the future.
Rollup Stack Secure Integrations
| Nitro V1 | OP V1 (trusted) | Nitro V2 | OP V2 | |
|---|---|---|---|---|
| Cert Verification | SequencerInbox | x | one-step proof | one-step proof: done in preimage oracle contract when uploading a blob field element |
| Blob Verification | one-step proof | x | one-step proof | one-step proof |
| Timing Verification | SequencerInbox | x | SequencerInbox | one-step proof (?) |
Trustless Integration Upgrade
Applies only to EigenDACertV4. “Trustless integration” = “secure integration”.
Overview
This section describes a schema for deterministically upgrading an eigenda blob derivation pipeline. The eigenda blob derivation pipeline contains two components:
- onchain: cert verifier and cert verifier router
- offchain derivation: kzg verification, recency check, altda commitment parsing and other logics defined in secure-integration.
Background
Consensus systems (L1/L2) typically upgrade logic via hardfork at block X:
- Before
X, old logic executes; afterX, new logic executes. - Software must be backward compatible (able to execute both logics) and enforceable (disallow executing old logic after X without stalling consensus).
Onchain Integration Upgrade
Integrations upgrade onchain logic by adding a new EigenDACertVerifier to a EigenDACertVerifierRouter. Each verifier has an corresponding activationBlockNumber (ABN) within the EigenDACertVerifierRouter. The router uses the DACert's reference block number to determine which verifier to use by comparing against its ABN. More see section contracts
This mechanism mirrors hardfork behavior: it is backward compatible and enforceable. Each EigenDACertVerifier also embeds a constant offchain derivation version, set at deployment, which governs off-chain logic.
Offchain Integration Upgrade
EigenDA blob derivation includes substantial off-chain processing. The offchain derivation version (uint16) versions the entire off-chain logic. For example, the recency window is 14400 when its offchain derivation version = 0; new versions may change the recency value, alter payload encoding, or introduce new new configs or validation rules.
To safely upgrade offchain logic, the L2 node’s eigenda-proxy must know when a new version becomes valid. With a new DACert type EigenDACertV4, this is enforced by requiring the certVerifier to check that the DACert’s offchain derivation version matches the constant value set by the contract. Once this check passes, off-chain code can safely use the offchain derivation version embedded in the DACert. Thus, onchain logic controls activation of offchain versioning, ensuring backward-compatible and enforceable upgrades.
Note
Each L2 should deploy its own router. Using the EigenLabs-deployed router delegates upgrade scheduling to EigenLabs. See contracts for router details and deployment guidance.
Rollup Stacks
OP Stack
Links:
Arbitrum Orbit
Our up-to-date Arbitrum Orbit docs for EigenDA V1 are available at docs.eigenda.xyz. EigenDA V2 support is currently work-in-progress; technical design updates can be found here.
We maintain fork diffs for the different arbitrum orbit repos that we fork:
ZKsync ZK Stack
ZKSync-era currently supports and maintains a validium mode, which means we don't need to fork ZKSync, unlike the other stacks.
The zksync eigenda client is implemented here. It makes use of our eigenda-client-rs repo.
EigenDA OP Secure integration
This document presents an overview on how EigenDA plugs into Optimism (OP) Stack.
writeandreadpath in a L2 rollup- Why the
readpath must stay live (even with a misbehaving op-batcher) - Adding an EigenDA stage to the OP derivation pipeline
- Hokulea, Rust library that defines and implements the Eigenda derivation rule
- How Hokulea works in both interactive fault-proof VMs and zkVMs
Write and Read path in L2 consensus
A rollup system can be split into two parts: write path to L1 and read path from L1
| Path | Direction | Purpose | Main actor |
|---|---|---|---|
| Write | L2 → L1 | Low cost L2 block production with user transactions | op-batcher + EigenDA proxy |
| Write | Direct on L1 | Censorship resistance + Deposit | Rollup users + Opimism Portal |
| Read | L1 → L2 | Safety – all nodes see the same block list | OP derivation pipeline |
- The
write pathensures the liveness of the L2 consensus. It consists of L2 batches produced by op-batcher and L1 deposit transactions. - The
read pathcontrols the safety of the L2 consensus. It ensures that all L2 consensus nodes see an identical list of L2 batches and L1 sytem and deposits transactions, such that an EVM can produce identical L2 state
If the read path stalls, honest nodes can’t reach the block height needed to dispute a bad state root.
L2 Write path (happy-flow)
- op-batcher bundles user txs.
- Sends compressed batches to EigenDA proxy, which converts them into an Eigenda blob. Proxy sends blob to EigenDA, and forwards the returned certificate to op-batcher
- EigenDA certificates are posted to the L1 Rollup Inbox.
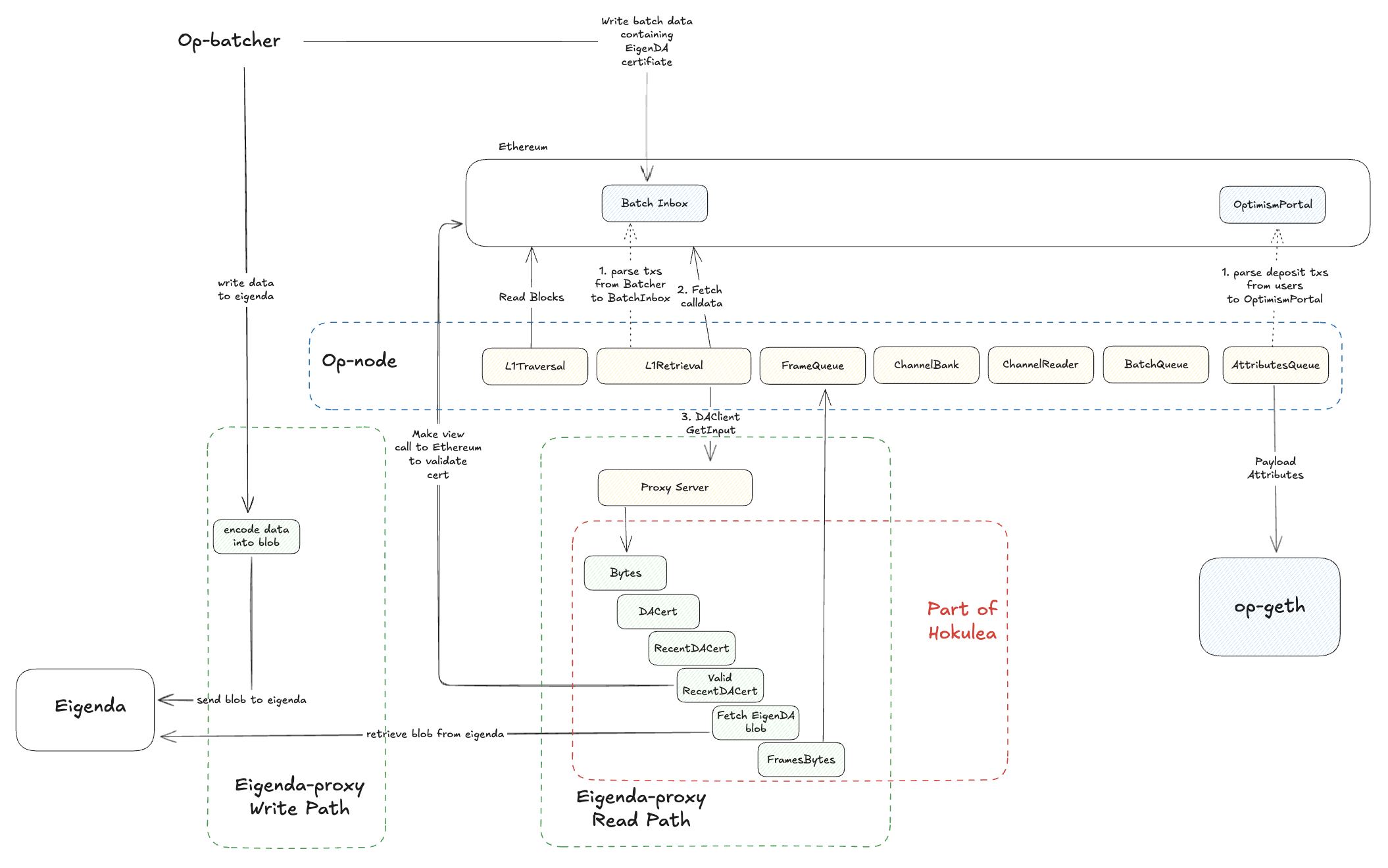
L2 Read path
The read path from L1 determines L2 consensus. OP has defined a derivation pipeline in OP spec. Both op-program in Golang and Kona in Rust implement the derivation pipeline. Like the diagram above, the derivation pipeline consists of stages that bring L1 transactions down to Payload Attributes which are L2 blocks.
To support secure integration, we have defined and inserted a Eigenda section in the OP derivation pipeline. In the diagram above, we have sketched where and what rules EigenDA inserts in the OP derivation pipeline. Both Eigenda proxy and Hokulea implement the eigenda blob derivation.
L2 Read path with EigenDA
As in the diagram, op-nodes use the read-path on the eigenda-proxy to fetch EigenDA blob. The proxy checks
- certificate has sufficient stake and is valid
- certificate is not stale
- retrieve & KZG-checked blob from EigenDA
- Decode and pass the data onward
More information can be found in the page secure integration. The key properties which EigenDA derivation strives to keep are
- Determinism – one unique blob per DA certificate.
- Liveness – discard anything that could halt the chain.
Both eigenda-proxy and hokulea hold those properties.
Proving correctness on L1
The security of rollup is determined by if there are provable ways to challenge incorrect L2 state posted on L1. In this section, we discuss our OP secure integration library Hokulea.
Short intro to OP FPVM
The correctness of a L2 state is determined by the derivation rules, which are implemented in both Go op-program and Rust Kona.
With interactive fault proof, the derivation logics are packaged into a binary ELF file, which can be run inside a FPVM (Cannon, Asterisc, etc.).
The FPVM requires both the ELF binary and data (L2 batches and L1 deposits) to be able to rerun the derivation pipeline. The idea is to repeat what op-node has done to reach consensus, except that in FPVM, every execution is traceable and challengeable.
Data is provided to FPVM in the form of preimage oracle. OP spec has defined rules such that all data in the preimage oracle are verifiable on L1.
Hokulea
Hokulea uses traits exposed by Kona derivation pipeline to integrate EigenDA as a Data Availability Source. Hokulea provides traits, implementation for EigenDA part of derivation pipeline, such that those logics can be compiled into ELF together with Kona.
Hokulea also extends preimage oracle for EigenDA, which is able to provide the verifiable interface for answering
- whether a DA cert is correct
- what is the current recency window to determine if a cert is stale
More information about the communication spec is at Hokulea. Both extension to preimage oracle and derivation logics allows for
- deterministically deriving a rollup payload from an EigenDA certificate
- discarding DA Certs that can stall the derivation pipeline
Canoe
We developed a rust library called Canoe that uses zk validity proof to efficiently verify the cert validity on L1 or inside a zkVM.
Hokulea integration with zkVM
Unlike interactive challenge game with fault proof, a zk proof has a property that only the honest party can create a valid zk proof with respect to the correct derivation rule. Hence, a malicious party can raise a challenge but is unable to defend its position.
- The Hokulea+Kona derivation is compiled into ELF for the needed environment (RiscV zkVM or one of the FPVMs)
- The Hokulea+Kona preimage oracle are prepared, where the validity of DA cert is provided by Canoe
- zkVM takes preimage and verifies it, then feeds the data into the ELF containing the derivation logics
- zkVM produces a proof about the execution
Hokulea is currently integrating with OP-succinct and OP-Kailua. For an integration guide, please refer to the preloader example for zk integration.
Rust Kzg Bn254 library
The constraint also requires all eigenda blob with respect to the kzg commitment in the DA cert. We developed a similar library to c-kzg called
rust-kzg-bn254 that offers similar functionalities as 4844 spec.
Hokulea
Hokulea provides a Rust implementation of EigenDA blob derivation for the OP stack. The Hokulea client (and its associated crates) implements the EigenDA blob derivation logic described in the EigenDA blob derivation section. The client is designed to be imported as a library into the OP consensus Rust implementation Kona.
Since the OP rollup inbox is not a smart contract, the secure integration requires EigenDA blob derivation to take place entirely offchain (see the design rationale in secure integration). Depending on the choice of VM and game type, Hokulea can support optimistic interactive fault proofs and ZK fault proofs, as well as validity ZK proofs.
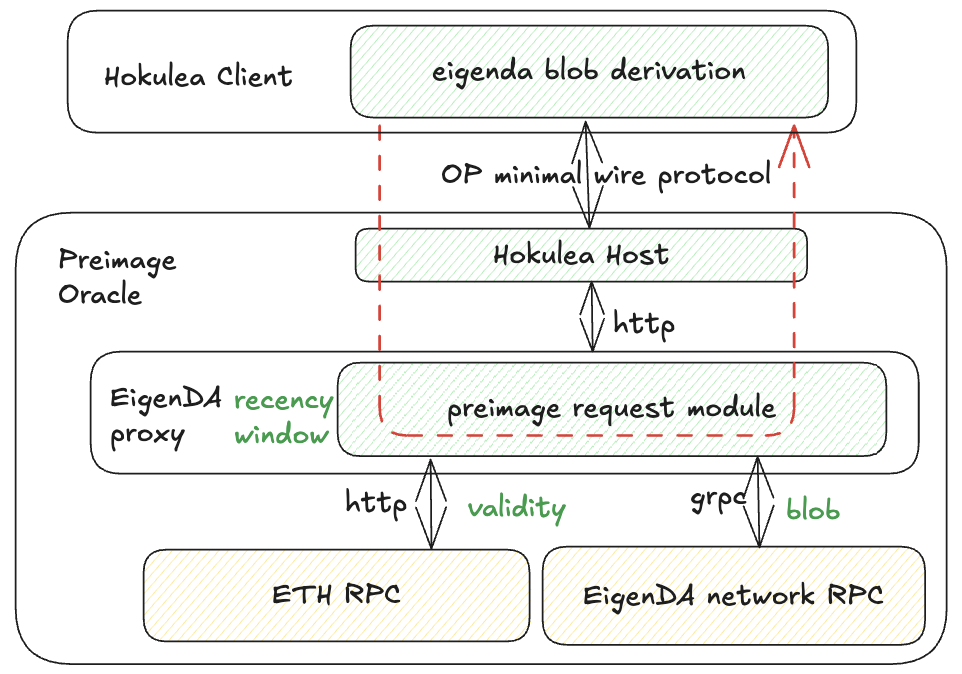
Preimage Oracle Architecture
In Hokulea, the interface is abstracted as a key-value map to make the preimage oracle verifiable on L1 Ethereum.
The Hokulea preimage host for the key-value oracle interface communicates with the EigenDA proxy (see diagram above). The proxy handles all the heavy lifting to retrieve the actual preimage data, while the Hokulea host serves as a thin layer that translates HTTP status codes into preimage data or errors.
Communication Between Hokulea Host and EigenDA Proxy
The proxy uses an HTTP interface to serve as a base layer for abstraction. The proxy exposes the following app-layer status codes in addition to HTTP status codes to convey information about the preimage:
| Message | HTTP Status Code | App-Layer Status Code | Indication |
|---|---|---|---|
| Decoded blob (rollup payload) | 200 | N/A | Successful request |
| Certificate validity | 418 | 1 | Certificate is invalid |
| Certificate recency | 418 | 2 | Certificate is too old |
| Encoded payload | 418 | 3 | Blob decoding error |
Encoded Payload vs. Decoded Blob
For developers familiar with the EigenDA proxy: on a default GET http query, the proxy returns the decoded blob (the rollup payload) as a byte string in an HTTP 200 response. However, to integrate the proxy as part of the preimage oracle for other Hokulea, the preimage data must be a valid blob polynomial where every 32 bytes is a valid field element on BN254 (the encoded payload).
The proxy must be able to return the encoded payload independently.
To eliminate redundant work that the upper layer (Hokulea host) would otherwise need to perform (the FFT step), the proxy needs to convert the EigenDA blob into encoded payload.
OP Optimistic Fault Proof with Cannon
This document explains how to integrate EigenDA blob derivation (via Hokulea) into the OP derivation pipeline and secure it with the default OP Fault‑Proof VM (FPVM).
Upgrade 16’s Interop Contracts proposal adds Kona fault‑proof programs to Cannon, enabling MIPS‑ELF binaries compiled from Kona. We therefore extend Kona with Hokulea so EigenDA‑based rollups can rely on the official OP fault‑proof system. Spec is still work‑in‑progress.
OP Fault‑Proof Recap
- Any party may dispute an L2 output by running op‑challenger.
- Players alternate moves within fixed clock deadlines; If the clock expires without a move, the last mover wins.
- A bounded game depth reduces the dispute to one VM step, which Cannon re‑executes—so every step must be fault‑provable.
L2 Consensus with EigenDA
| Component | Purpose | Executed in |
|---|---|---|
| Kona | OP derivation pipeline | Cannon |
| Hokulea | EigenDA blob derivation | Cannon |
Both parts compile into a single MIPS‑ELF. Cannon runs it whenever a challenge is raised.
Proving one Instruction in EigenDA Blob Derivation on L1
| Type of VM Instruction | Verification type | Handling |
|---|---|---|
| Execution step | Logic | The MIPS instructions are implemented in the smart contract to re-execute any processing logic (e.g., any incorrect execution when converting an encoded payload to a rollup payload) |
| Preimage lookup | Data | Requires correct key–value pair on L1 Preimage Oracle contract |
When the disputed instruction is a preimage lookup, the player must first submit the correct key-value pair to preimage oracle contract, and then resolve the final instruction. The Preimage Oracle will disregard any submitted value if the required key-value pair relation does not hold. If a party fails to provide a valid preimage before its timer expires, that party forfeits the game.
Onchain Pre‑Image Infrastructure
Cannon relies on PreimageOracle.sol:
mapping(bytes32 => uint256) public preimageLengths;
mapping(bytes32 => mapping(uint256 => bytes32)) public preimageParts;
mapping(bytes32 => mapping(uint256 => bool)) public preimagePartOk;
EigenDA blob derivation requires three pre‑images:
- Certificate validity
- Point opening on blob
Keys of the preimages are keccak256(address) of the reserved addresses (prefixed as type 3 per the OP spec).
The preimage and relation between (key-value) pair can be specified by a contract that:
- uses certVerifier Router to establish the validity of the DA certificate, the preimage is a boolean;
- verifies KZG point openings on a blob (using EigenDA’s
BN254library), the preimage is 32 bytes from the EigenDA blob;
OP‑Challenger Duties
- Logic steps: automatically prepares proof data for re-executing the MIPS instruction
- Pre‑image steps: downloads the blob from EigenDA, constructs a point‑opening proof, and submits the pre‑image to L1.
This integration ensures every logic or data step is fault‑provable, allowing EigenDA rollups to benefit from the official OP security model.
Arbitrum Orbit Secure Integration with EigenDA V2 and ALT DA Interface
The EigenDA integration's team is currently working on a secure integration design with Arbitrum's upcoming ALT DA spec. This page will be updated over time as design updates are made.